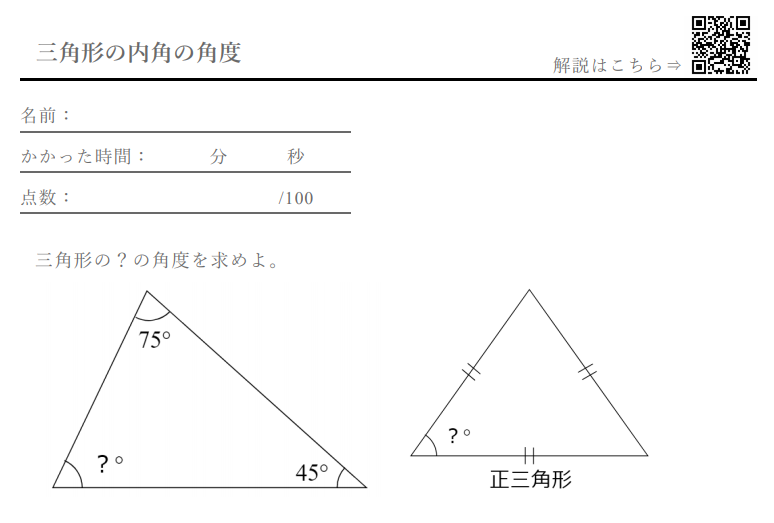
三角形の内角 三角形の3つの内角の和 → 必ず180°になる 問題 xの角度は??簡単だね?3つの内角を全て足し算すると180°だから、 40°65°∠x=180° ∠x=75° ・・・(答え) 三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ! 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでAの角度は、360°(72°38°30°)=2° よって、 答え A=2 °角度の求め方(第2 回 な図形では対応する角度の大きさが等しいので、下の図のように水色の直角三角形の の角度はと黄色の直角三角形の角EFCと等しくなります。 このように、 合同な図形を見つけて、対応する角をみつけることが、問題を解く第一ステップとなります。 p合同とは回転し
直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora
三角形 角度 求め方
三角形 角度 求め方-S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B 直角三角形で三平方の定理をつかっているから なんだ。 長方形で対角線をひいたら、 2つの三角形にわかれるでしょ?? そのうちの1つの直角三角形をえらぼう。 そいつで、 三平方の定理をつかって対角線の長さを求めるんだ!




中2 数学 4 2 三角形の角度の利用 Youtube
紙に書いた三角形を切って確認することですが ここではもう少し論理的に確認していこうと思います。 上の図は適当に書きましたので、 私にもそれぞれの角度がどれくらいか分かりません。 でも、内角の和は求められます。 どのように内角の和を求めればいいのでしょうか? ヒントは (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは,三角形の内側の角の大きさの和のこと直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「=11*SIN(RADIANS (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン(arcsin、逆正弦)、アークコサイン (arccos、逆余弦)、アークタン
・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度 三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a: 角度θ: 度 ラジアン 底辺aが1、角度θが30°の直角三角形 高さ b: 斜辺 c
斜辺の長さをr,他の辺の長さをx,y とするとき, y r, x r, y x, の値は,三角形の大きさに関係なく,角θの大きさだけで決まる。 これらを,それぞれθの 正弦(sine), 余弦(cosine), 正接(tangent) といい,sinθ, cosθ, tanθと表す。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75° ここで、三角形 \(abd\) に注目すると、以下の4つの式が成り立つことが分かります。 円周角の定理 から \(∠ADB=∠ACB\) タレスの定理(直径に対する円周角は直角)から \(∠ABD=90°\)



円と三角形 角度 中学から数学だいすき
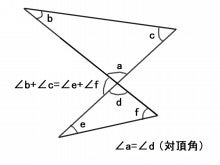



角度の求め方 数学が嫌いなんです
3年算数三角形教え方のポイント ① 三角形の仲間分け ② 二等辺三角形・正三角形の理解 ③ コンパス・定規を使っての二等辺三角形・正三角形のかき方 2年生の三角形の勉強 は 直角のところをみていました が、3年の三角形の勉強は、 辺の長さを特にみRight triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お客様の声三角形における三角比の値 ABCでcosB の値を求めよ。 という問題で,cosB =3/2 と答えてしまいました。 sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
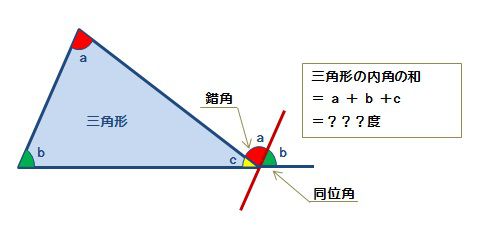
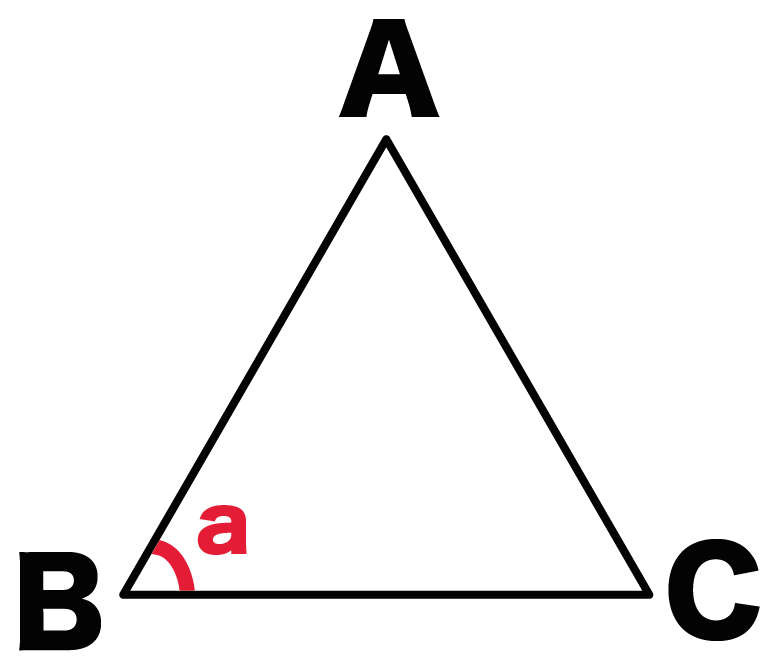
すると角aは三角形イ、ウ、エの外角になっています。(旗が逆さになっています) 三角形の内角と外角の関係から = + 角A = 30°+ 90° = 1° と計算できます。 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




中2 数学 4 2 三角形の角度の利用 Youtube
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま緑 正弦定理 (はじめに) 三角形を表すとき 多くの場合、頂点の名前は A , B , C の順に左回りに付けます。 辺の名前は「向かい合う角」の小文字で表します。 したがって、 A の対辺 BC を a とします。 同様にして、特に断り書きがなければ b=AC , c=AB になります。 頂点の名前 A , B , C でその内角∠ A 、∠ B 、∠ C の大きさを表し、単に sin A , sin B , sin C などと書き この記事では、三角関数について、角度の求め方や変換公式(\(90^\circ − \theta\) など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね!




角度の問題まとめ 無料で使える中学学習プリント



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局
つまり、角度をもとに辺の比を求めているわけです。 それに対し、逆三角関数は「底辺と対辺の比が なら、その辺に対する直角三角形の角は30°になる」ということを表しています。 逆三角関数の考え方 図1を使って、逆三角関数を考えてみましょう。 三角関数の角度を求めるときは、θの範囲を忘れないこと それぞれの求め方をまとめると 単位円 を書いて、三角関数に適した直線を書き込み交点を求める。 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるか 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な




タンジェントとは何か 中学生でも分かる三角関数の基礎
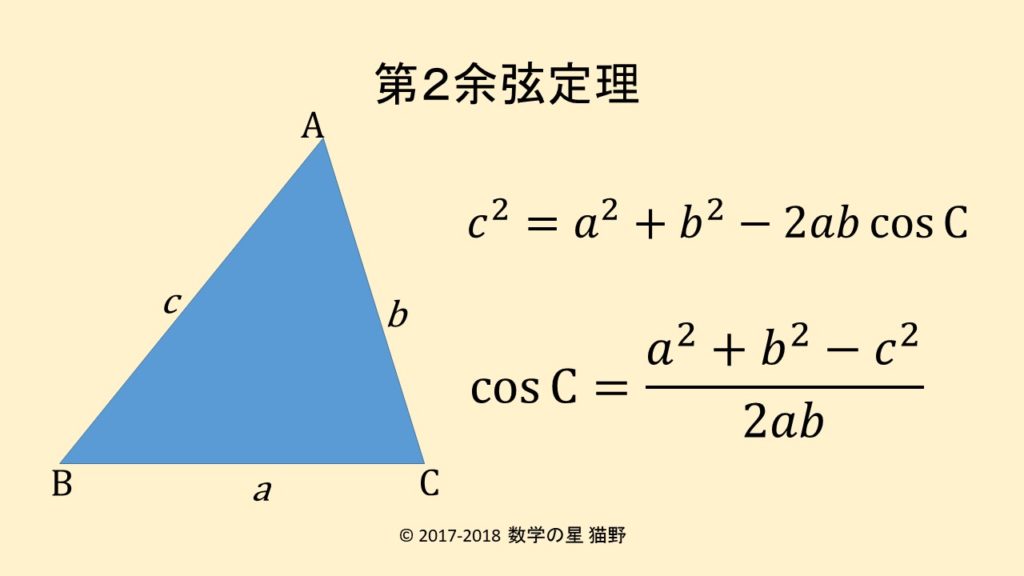



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
三角形、四角形、角、面積 円、三角形、四角形の面積を計算できるようになろう。 角度のはかり方もいっしょにおぼえてね。 動画で学ぼう! (NHK for School) 三角形の面積の求め方を、四角に直すことで原理から考える。 結婚式場から指輪が盗まれた 高校までの範囲ならば、辺の長さが実数で与えられているはずなので特殊な角度だけ覚えておけば大丈夫だと思います。 arctan 0 = 0 arctan 1/√3 = π/6 arctan 1 = π/4 arctan √3 = π/3 (2) 辺cの値を求めます。 直角三角形であるので、 c = √ (a^2 b^2) となります。 cosθ1 = a/c より、 θ1 = arccos a/c となります。 また、 cosθ2 = b/c より θ2 = arccos b/c となります。 (1)と求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




三角形の3辺から角度を計算 高精度計算サイト
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ 折り返し角度問題のポイントはこれ 算数解法の極意 角度を求める問題 中学生 難問 ラングレーの問題 整角四角形 図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に 中学受験 図形の角度問題は 7つ道具 で攻略 かる




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




角度の求め方 算数の教え上手 学びの場 Com



1



3




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学



直角三角形の解法 1




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
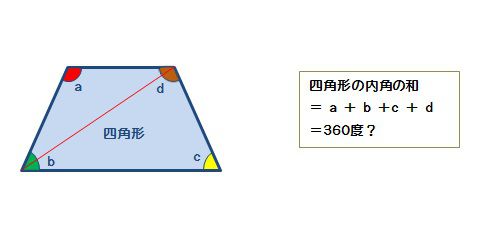



四角形の内角の和 算数の公式覚えてますか



1




三角形の辺から角度を計算 製品設計知識




正三角形や二等辺三角形の内角 Youtube
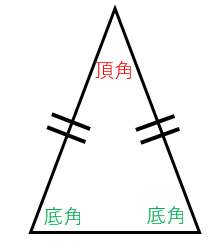



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学
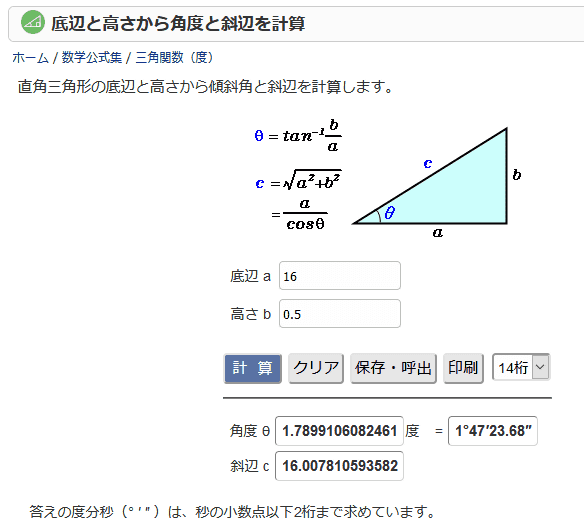



表計算ソフトを使って 底辺 と 高さ から 角度 を求める



内接円 内心




余弦定理で角度を求める方法 数学の星




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf
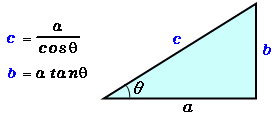



角度と底辺から斜辺と高さを計算 高精度計算サイト




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
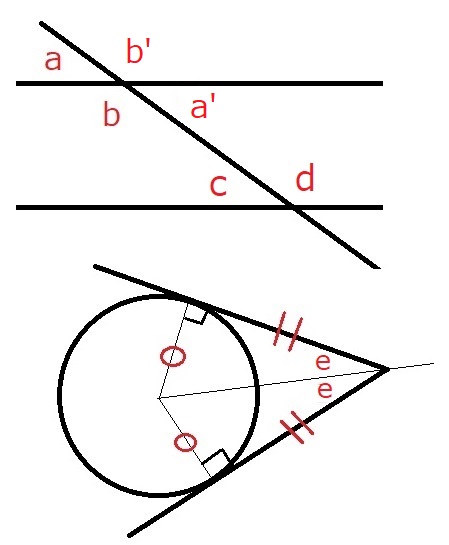



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明




三角形の角度を求める問題 小学生 中学生の勉強




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe



1




角度の求め方 角度の求め方 Mqttk




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター



三角形の内角の和 算数の公式覚えてますか



角度の求め方 算数の教え上手 学びの場 Com




角度の計算 裏技まとめ 教遊者



三角形の内心の証明と頻出例題2問 具体例で学ぶ数学




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット



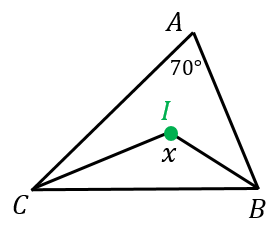
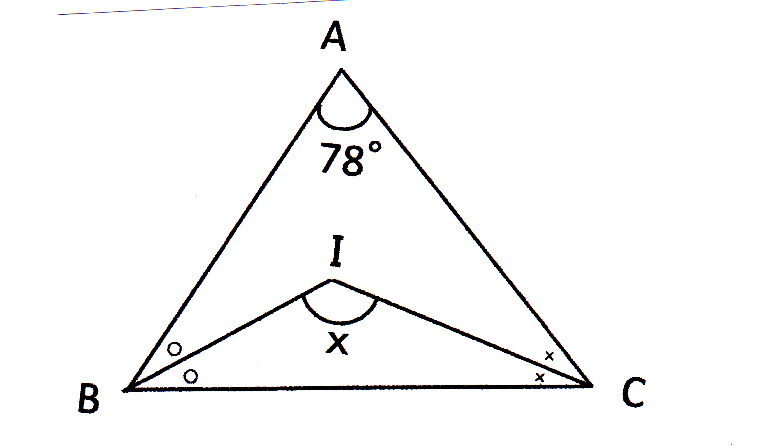
点iはこの三角形の内心である 点iのなすaの角度は何度か 求め方教えて Yahoo 知恵袋



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora



Math 平行と合同 角の二等分線と角度 働きアリ



円と三角形 角度 中学から数学だいすき



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
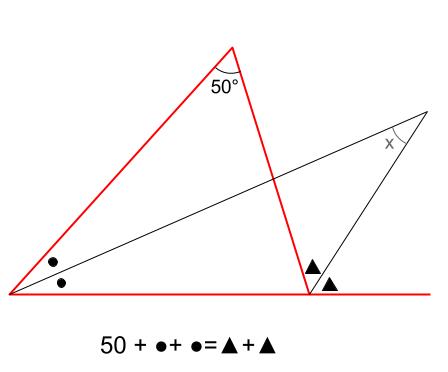



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




あ かまでの角度を求めてください 急いでます 教えてください Clear
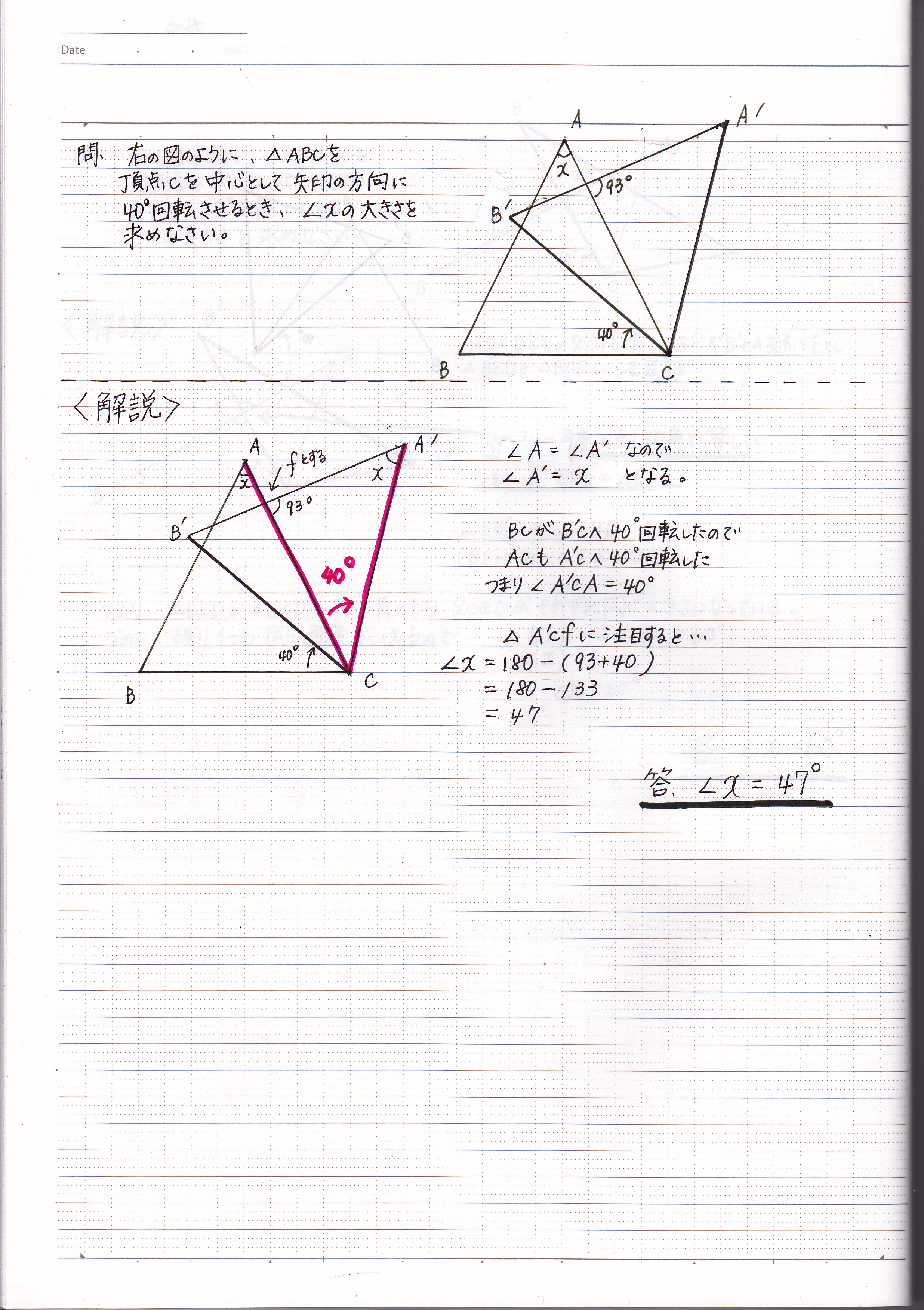



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
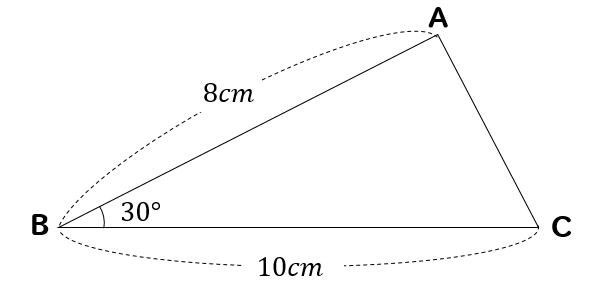



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



普通の電卓で計算できる直角三角形の近似計算




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
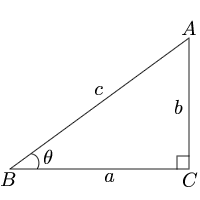



三角関数から角度 逆三角関数 三角形の計算 計算サイト



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




角度の求め方 算数の教え上手 学びの場 Com




小5 算数 小5 31 三角形の角度 Youtube



三角形の角度を求める 思考力を鍛える数学



三角形 の内角の角度 計算ドリル 問題集 数学fun




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
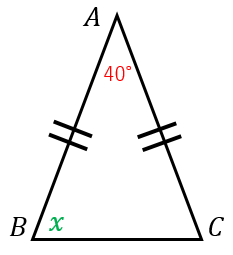



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学
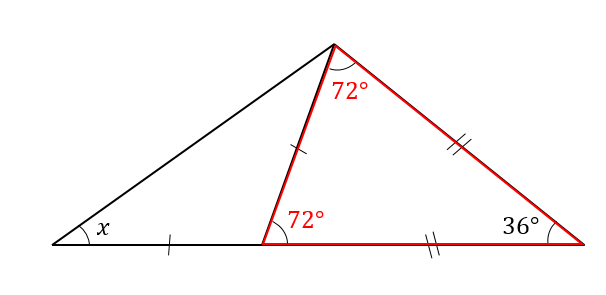



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
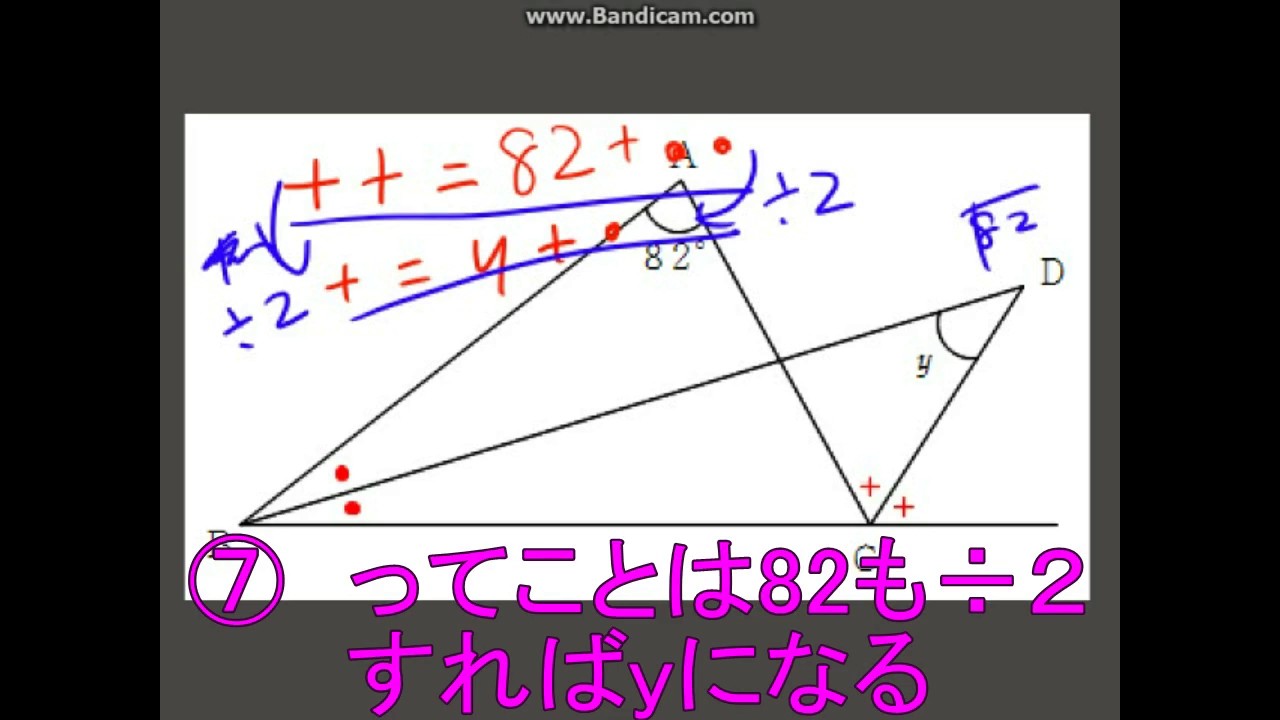



中学二年 数学 三角形の角度の求め方 中の上編 Youtube




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト
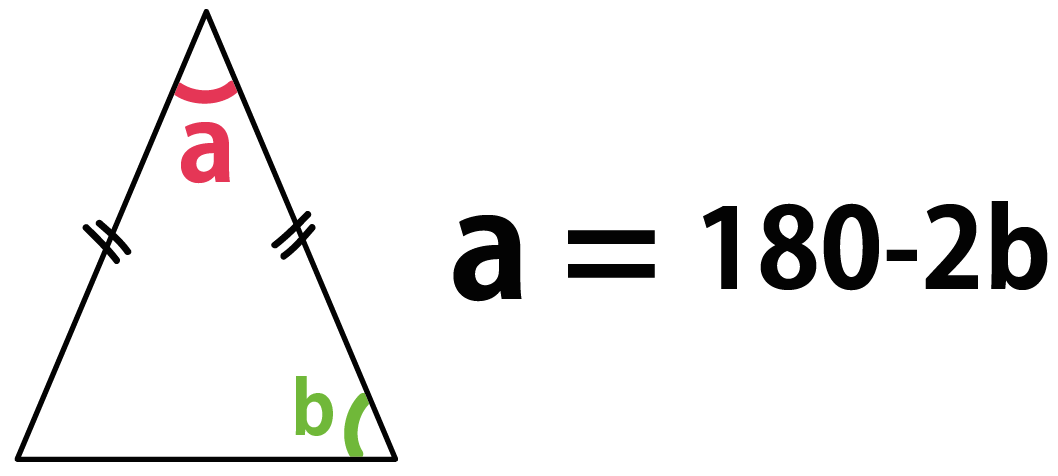



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




数学 中2 53 角度チャレンジ Lv 1 Youtube




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
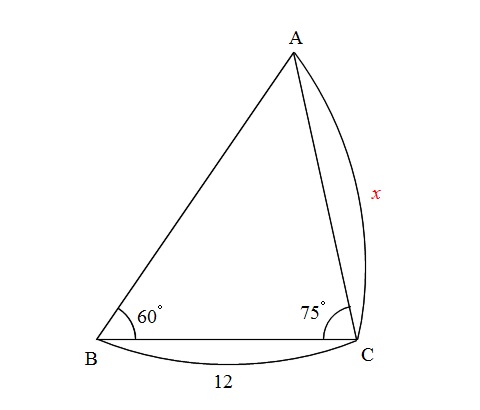



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない
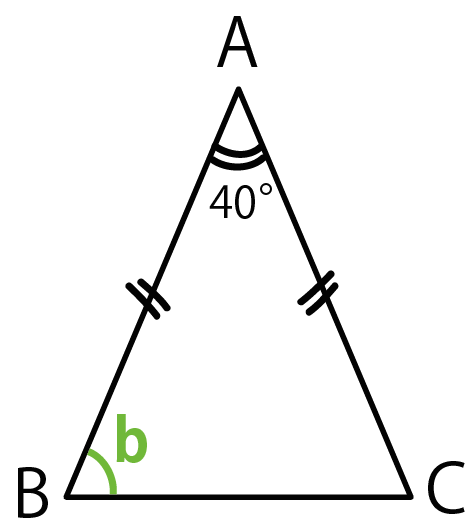



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




三角形の角度を求める問題 小学生 中学生の勉強




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



内接円 内心




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の角を求める Youtube



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明
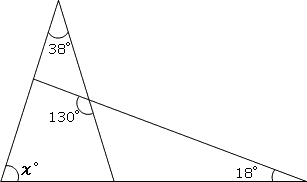



角度の求め方 算数の教え上手 学びの場 Com




小5 算数 小5 31 三角形の角 Youtube
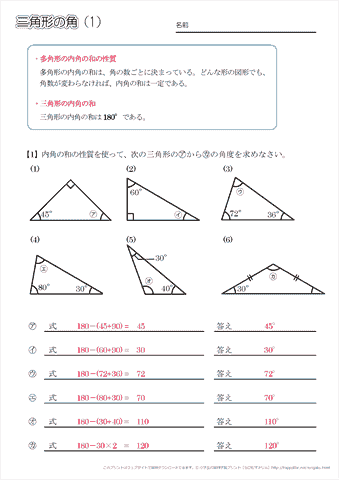



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題




黄金三角形による18 シリーズの三角比 おいしい数学




点oが三角形abcの外心であるときのaの角度の求め方を教えてください Clear




底辺と高さから角度と斜辺を計算 高精度計算サイト


