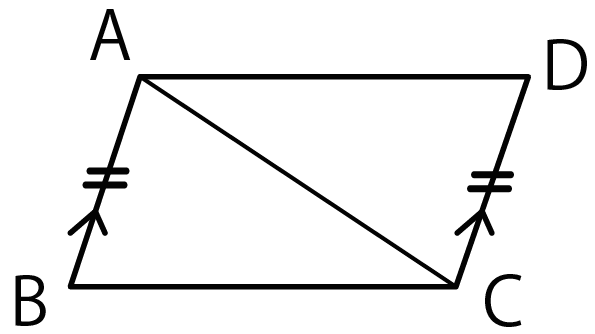
三角形の形状・証明問題 == 《解説》 三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です.2 つの辺が等しい三角形を二等辺三角形という(定義 ていぎ)。 右図のようなab=ac の二等辺三角形で, ∠aを 頂角 ちょうかく ,頂角に対する辺bcを底辺 ていへん , 底辺の両端の∠bと∠cを 底 てい 角 かく という。 問題(後期期末)三角形の合同の証明 基本問題1 図でAC=DB, ∠ACB=∠DBCのとき, ABC≡ DCBを証明せよ。 A B C D 図でAB=DC, AC=DBのとき, ABC≡ DCBを証明せよ。 A B C D 右の図でAC//BD, AD//BCのとき, ABC≡ BADとなることを証明せよ。 A B C D

世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル
三角形の証明 問題
三角形の証明 問題-\(\triangle ABC\) が二等辺三角形であることを証明せよ三角形が二等辺三角形であることを示したいとき、・\(2\) つの辺が等しい・\(2\) つの角が等しいのどちらか片方がいえればOKです。これも暗記ですよ。三角形の合同条件を暗記したの同じように。== 正弦定理・余弦定理の応用三角形の証明問題 == 《解説》 正弦定理・余弦定理の応用として,辺と角度を含む式を証明する問題があります.次の例のように,「 ABCについて,...が成立することを証明しなさい」という形で指示されているときには,特定の形の三角形ではなく,「すべて




数学の証明問題 数学の証明問題の解答を見出せずに悩んでいます 問題は二 Okwave
FdData 高校入試:中学数学2 年:三角形と四角形 仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/三角形の合同を証明する問題 ポイント 角度や辺が等しいことを証明する問題 会員登録をクリックまたはタップすると、 利用規約・プライバシーポリシー に同意したものとみなします。 ご利用のメールサービスで @tryitjp からのメールの受信を許可して2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ③ 3 下の図のようなAB=ACの二等辺三角形ABCがあります。
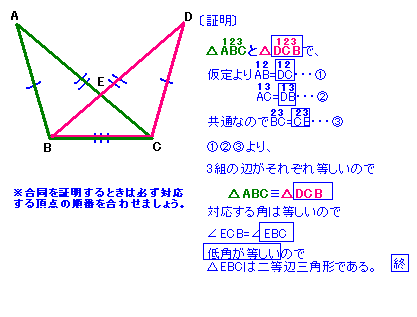
10/5/17 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、証明問題で二等辺三角形があるとき 証明問題で二等辺三角形があるとき、 どの \(2\) 辺が等しい二等辺三角形なのか、情報が与えられます。 そのとき、 「二等辺三角形なので、底角は等しい」 は証明なしで使ってOKです。三角形の合同の証明 三角形の合同の証明③ 下の図で,ac°db,cm=dm である。 このとき,¼acm×¼bdm であること を右のように証明した。下線部をうめて, 証明を完成させなさい。 三角形の合同の証明④ 下の図で,ab°dc,ab=cd である。
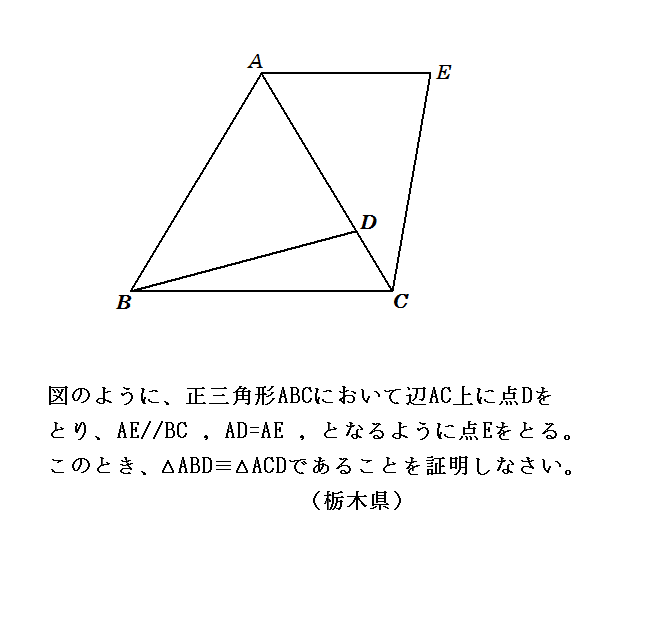
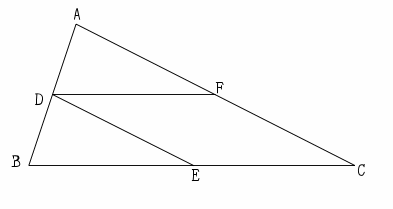
正三角形の証明問題1 名前 右の図のように、正三角形abc の辺ab, ac上に a それぞれ db=aeとなるような点d,eをとるとき、 dc = ebになることを証明しなさい。 e d b c 右図で、 abcと ecdが正三角形である a とき、ad = eb であることを証明しなさい。 e b c d15/2/21 二等辺三角形の定義、定理、基本的な証明問題の練習プリントです。定期テストにもよく出題されますので、確実に出来るようにしましょう。 二等辺三角形の定義「二つの辺の長さが等しい三角形」 等しい二辺の間の角を頂角という。 頂角に向い合う辺を底辺という。反射テスト 証明問題 三角形 五心とその関係 02 1 をうめよ(s 級2 分30 秒;



中2数学 直角三角形の合同の証明のポイントと練習問題 Pikuu




中二 数学 直角三角形の合同 この証明問題の の意味がわかりません W Clear
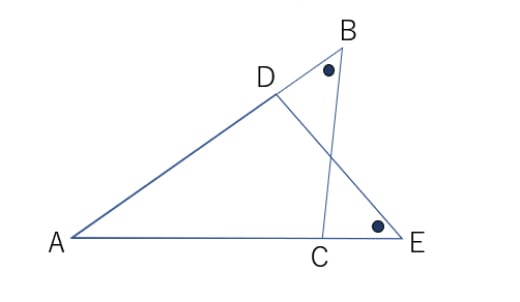
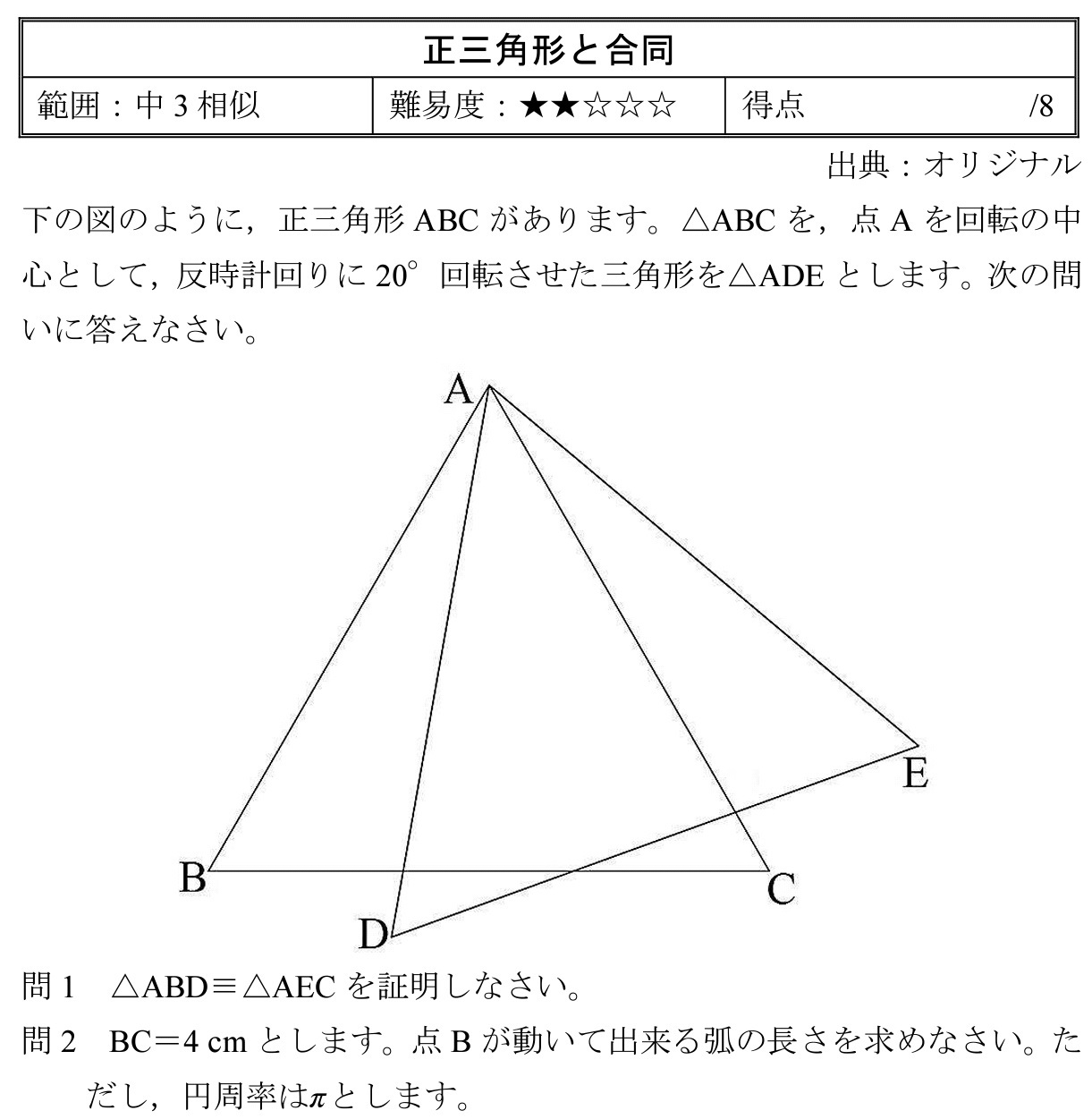
C 級8 分) a b c i s u t ★三角形の内心 三角形の内心は;2年生 5 図形の性質と証明 (2) (1)とは別の三角形に着目して,証明することにしました。 ACDと ABEに着目して, CD=BEであることを証明しなさい。 (3) この問題で,CD=BEは常にいえることがだんだん色々な問題を紹介するようになりましたが。 今回は,初心に戻って,非常に図がシンプルだけど,何かキツイ問題です。 北海道は,図がシンプルで,証明の書く量もそこまで多くないですが,何か難しい! 第27回芸術的な難問高校入試 「どの三角形」 出典:17年度 北海道 過去問: http//wwwkoukouhokkaidocedjp/gakuryokukensa/h30gakuryokuhtml 範囲:証明 難易度



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 合同の証明 働きアリ



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
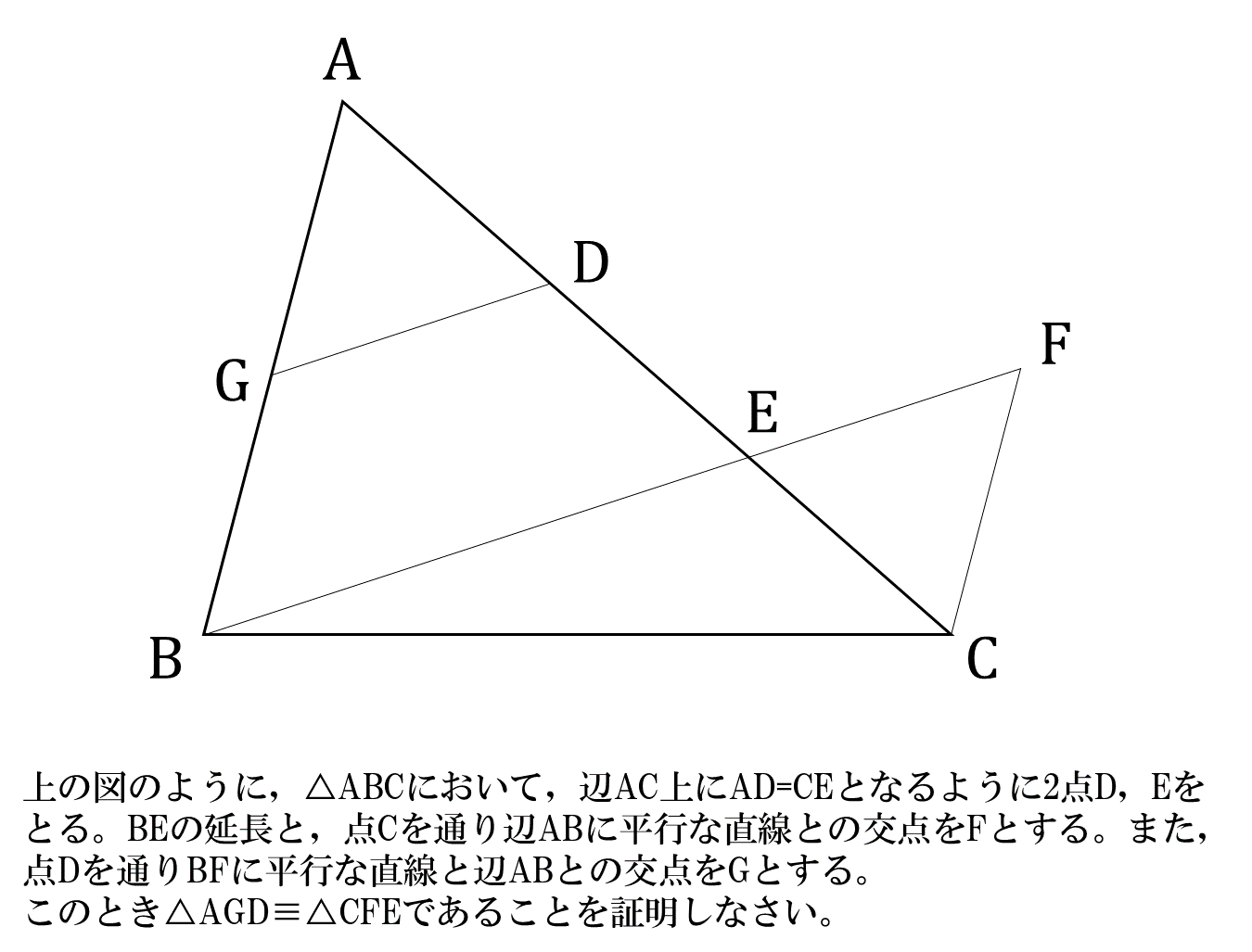
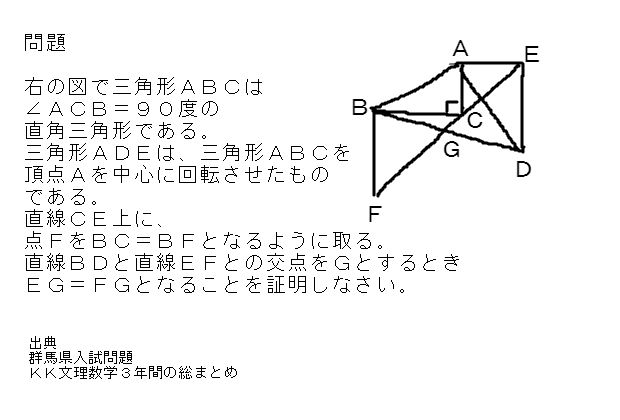
合同とは? 三角形の合同条件1(3辺) 三角形の合同条件2(2辺とその間の角) 三角形の合同条件3(1辺とその両端角) 仮定と結論;問題 問題のヒント 角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 難問5の証明;三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnとして、直線nと∠BCAの二等分線との交点をF,直線nと∠ACEの二等分線との交点をGとする。 FD=DGと




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル



数学 中学証明問題を解く4つのポイント
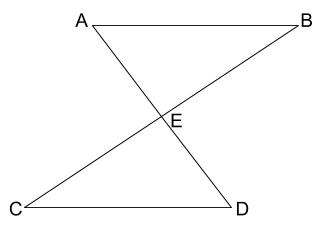
3 つの角の二等分線は必ず1 点で交わる 証明 問題 三角形abcがある。辺ac上に点dをとり、点dを通る線で三角形abcを折り、点aを辺bc上に重ね、重なった点を点eとする。点dを通る線と辺ab上の交点をfとする。 ∠afd=∠febのとき、 cdeは二等辺三角形となることを証明しなさい。 ⇒解答例はこちら(jpg画像)1 右の図でBDは∠ADCの二等分線で、 AD=BD、∠CAD=∠CBDである。 このとき AED≡ BCDとなることを証明しなさい。 A B C D E 2 図で点Dは辺ABの中点で、DF//BC、DF=BEとなって いる。 このとき ADF≡ DBEを証明せよ。



三角形の合同 証明の問題 高校入試 ネコネコ算数数学ページ




正三角形の合同証明 無料で使える中学学習プリント
だけど、しっかりとした手順を身につけてもらえれば、すっごく簡単に解くことができるようになるよ! 今回の記事では、三角形の合同を証明する問題を基礎からみっちりと解説していくね! それでは、次の問題を利用して証明の書き方について解説していきます。 下の図で、AB=AD、BC=DCならば、 ABC≡ ADCとなることを証明し第5章 図形と相似 <前: L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答 :次> 練習問題1 以下の1~3に示した各組の三角形が相似であることを証明しなさい。 (※辺の長さの単位はcm) 1 ABCと EDC 2 ABCと AED 3 ABCと EBD二等辺三角形・直角三角形の定義:合同条件と証明問題 中学数学で学ぶ図形に二等辺三角形と直角三角形があります。 二等辺三角形と直角三角形は特殊な三角形だといえます。 特殊な三角形なので、それぞれ特徴があります。 どのような特徴があるのか学ぶことによって、角度を計算したり、図形の証明を行えたりできるようになります。 二等辺三角形と直角




証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト
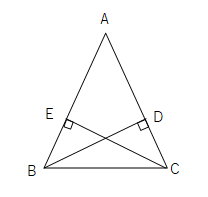
ABが∠CADの二等分線で、∠ACB=∠ADBのとき CB=DBとなることを証明せよ。 2 ∠AED=∠ACB、AD=ABのとき DE=BCを証明せよ。 3 BDが∠ADCの二等分線でDE=DC, ∠DAE=∠DBCのとき AD=BDを証明せよ。 4 GD//BFで、GD=FE, AD=CEのとき 正三角形を含む図形の三角形の合同証明の問題です。 正三角形は 三辺が等しい 3つの角度がすべて等しい (すべて60°) であることを利用して、等しい辺、等しい角を探していきます。(2) 「2 角が等しい三角形は二等辺三角形である」ので, bae は二等辺三角形でba=be=5cm ゆえに,ec=bc-be=7-5=2cm 問題(3 学期) 右の図の平行四辺形abcd で,∠bad の二等分線 と辺bc の交点をe とするとき,次の各問いに答えよ。 (1) abe はどんな三角形か。




三角形の合同条件と証明問題の解き方 数学fun



中2数学 直角三角形の合同証明のポイントと練習問題 Atstudier



直角三角形の合同証明 難 の解説 春日井市高蔵寺の学習塾 西村セミナールーム




中2数学 二等辺三角形の証明 練習編 映像授業のtry It トライイット



直角三角形の合同 証明問題 苦手な数学を簡単に



4gr7x76yz2id1fo99eleb Com Benkyou Suugaku Syoumei Html




直角三角形の合同の証明の問題です わからないので教えてください お願いします Clear




中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室




二等辺三角形と証明 Youtube
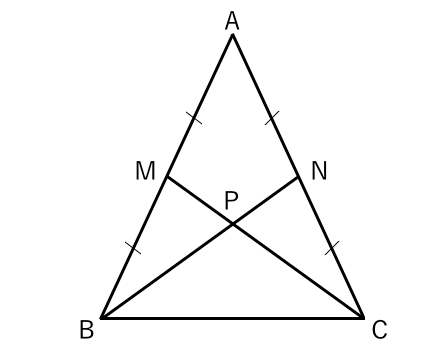



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




世界一わかりやすい数学問題集中2 5章 図形の性質と証明



1




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題




中2数学 二等辺三角形の証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
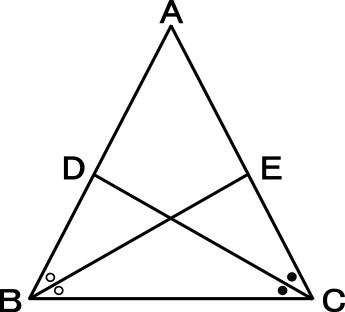



中学2年数学練習問題 図形と合同 三角形の合同の証明問題
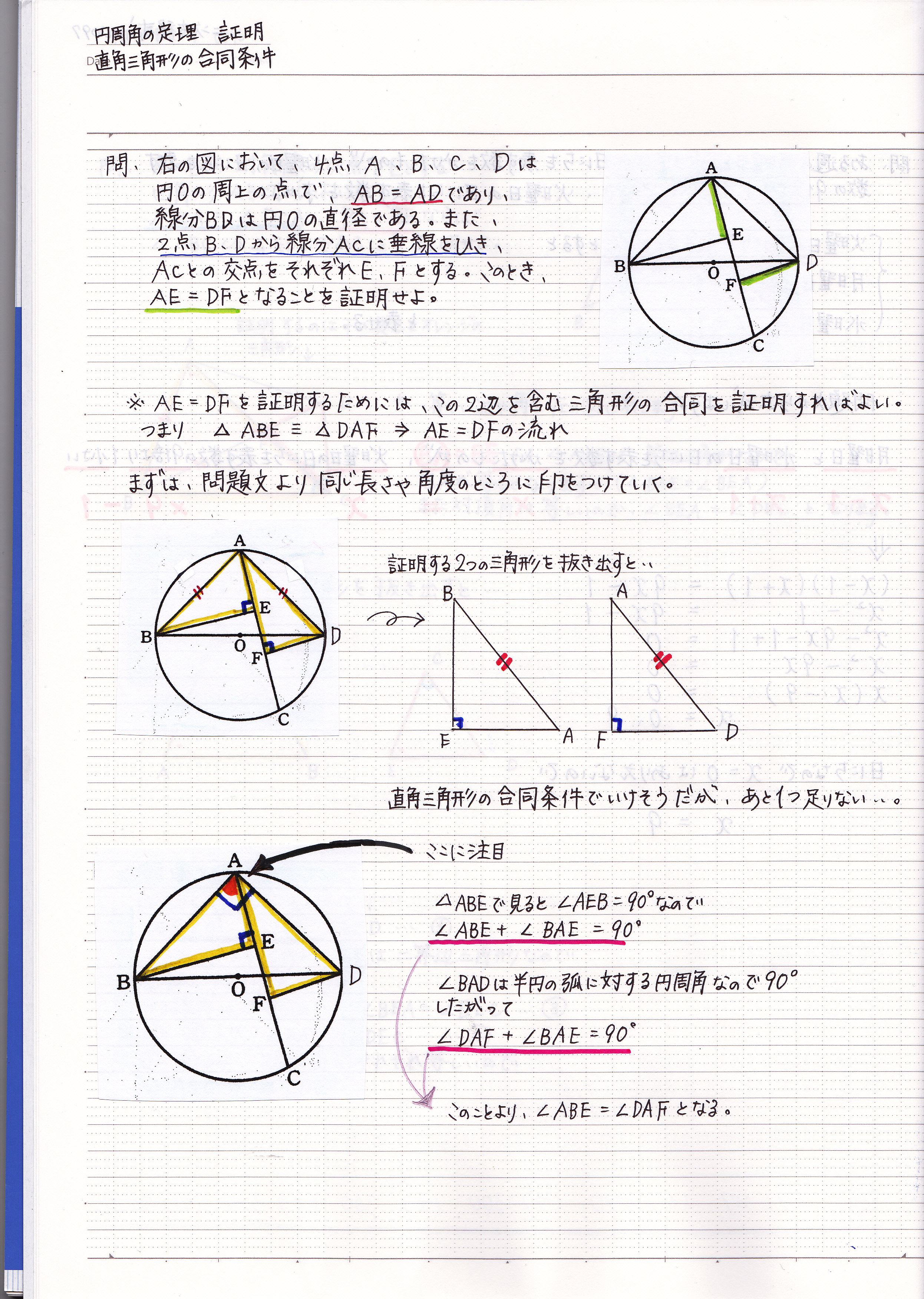



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
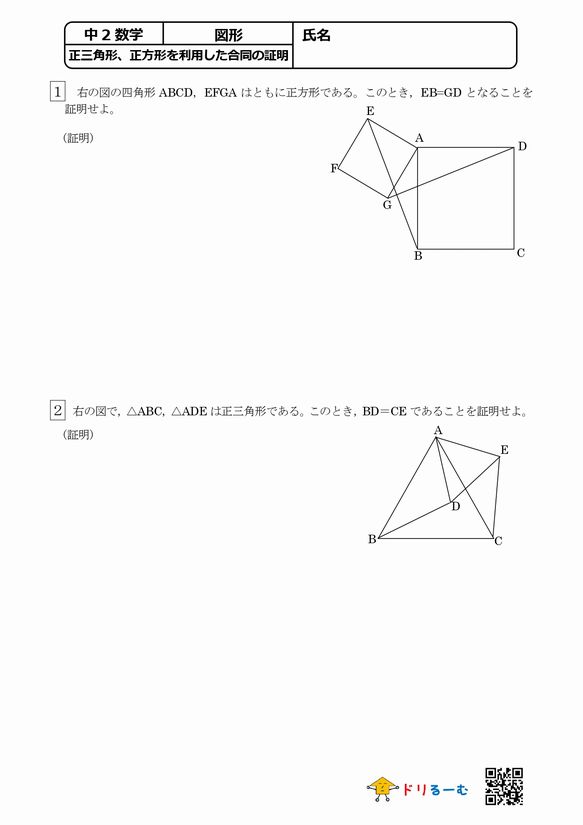



正三角形 正方形を利用した合同の証明 ドリるーむ
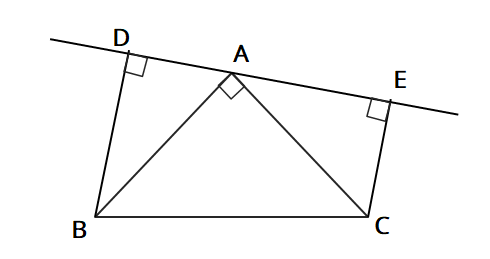



中2数学 直角三角形の合同の証明 応用問題 中学生勉強サイトあかね先生
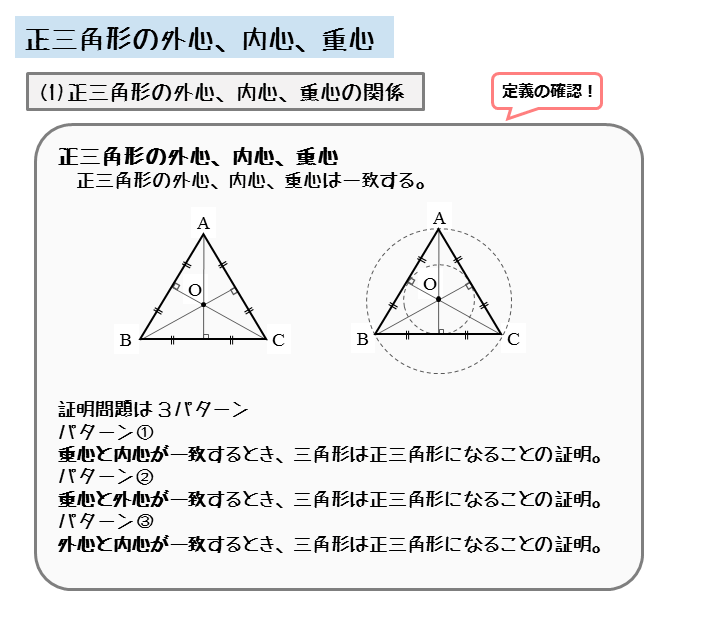



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




直角三角形を使った証明 Youtube




無料 中2数学 発展問題 解答プリント 228 三角形 四角形1 二等辺三角形



Math 平行と合同 証明の書き方 2 よく出る問題 働きアリ The 2nd




中3 相似証明問題 この下のような証明問題の場合どことどこの図形でやるか Okwave
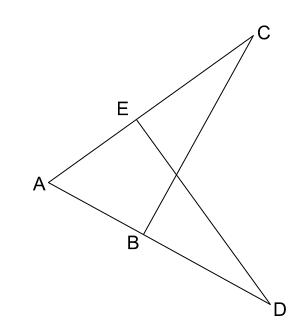



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su




合同の証明 清水塾



1



3




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
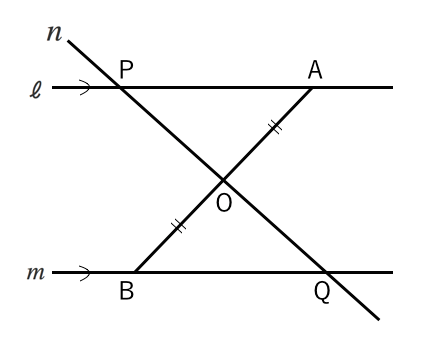



合同な図形 三角形の証明問題 苦手な数学を簡単に



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
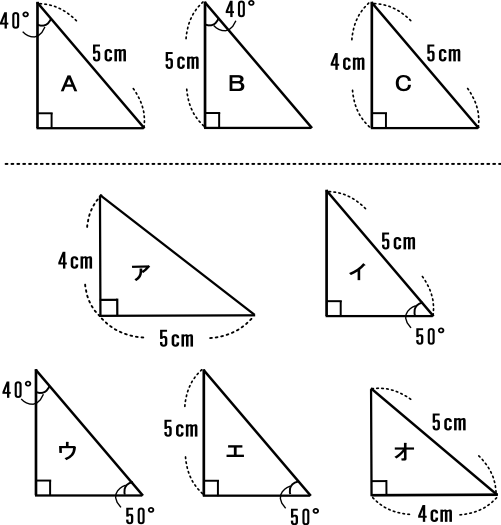



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の相似条件と証明問題の解き方 数学fun




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




直角三角形と証明 Youtube
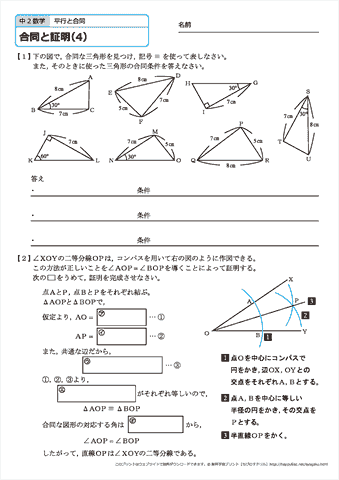



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張
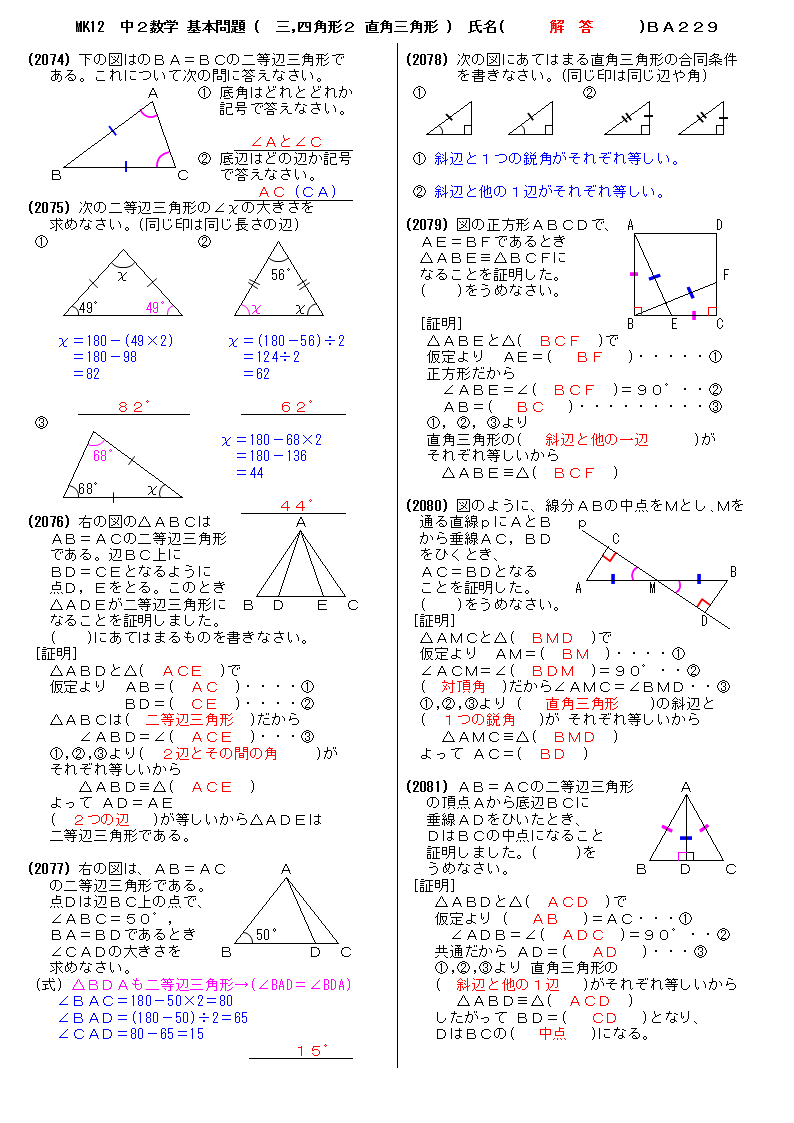



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
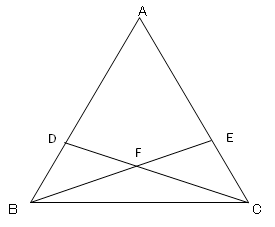



三角形の合同 3 ネット塾




二等辺三角形になることの証明 Youtube




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




まる先生 Marusensei8 証明 は3つの証拠をさがそう 1 2 まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 まる練数学 中学数学 証明問題 三角形の合同 Nitter



中学数学 証明問題のやり方は 解き方のコツや図形問題への対処法を解説 学びtimes
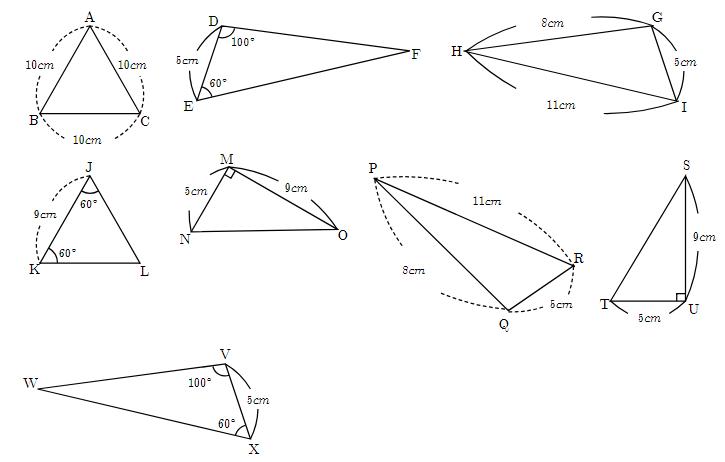



中2数学 三角形の証明の仕方 Pikuu
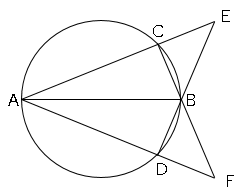



直角三角形と円周角の定理を利用した合同の証明問題 数学の要点まとめ 練習問題一覧




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




三角形の重心 定義と性質を証明問題と座標を用いる例題で解説 高校生向け受験応援メディア 受験のミカタ
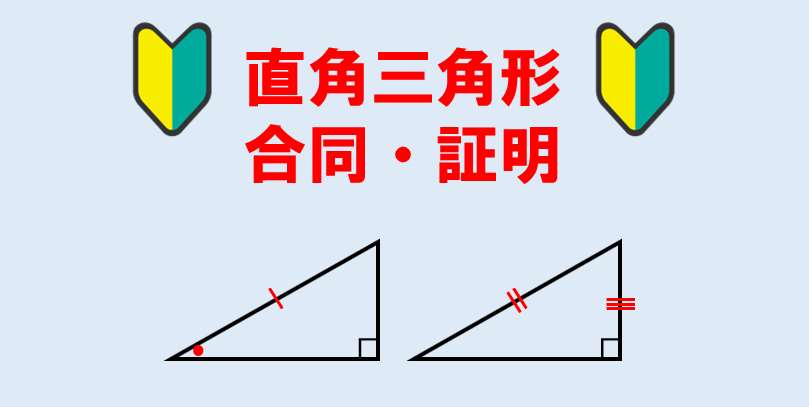



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



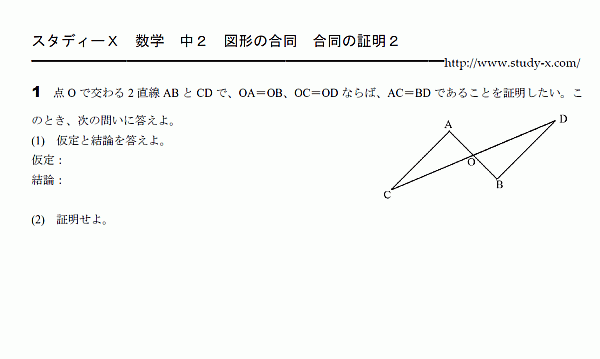
合同の証明2
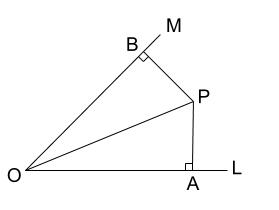



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ



中2 数学 無料学習プリント教材




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




三角形の合同証明の練習 無料で使える中学学習プリント




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



4gr7x76yz2id1fo99eleb Com Benkyou Suugaku Syoumei Html



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



1




中2数学 正三角形の証明 練習編 映像授業のtry It トライイット



U9j580gf8iba369ji2w Xyz P 970




中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath




中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット



直角三角形の合同条件を使った証明問題の解き方 2 現役塾講師のわかりやすい中学数学の解き方



訂正 正三角形と合同 高校入試 数学 良問 難問



中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生




都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法




中2 三角形の合同を利用した証明問題 発展編 これで受験バッチリ 中学生 Clear




数学の証明問題 数学の証明問題の解答を見出せずに悩んでいます 問題は二 Okwave




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



二等辺三角形の性質を利用した合同の証明 チーム エン



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor



三角形の合同の応用問題 制限3分 中学数学 理科 寺子屋塾の復習サイト



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su



Katekyo学院山形 中学生 証明問題 21 1 27




中学数学 証明 証明が苦手な中学生さんへ 家庭教師が教えるコツとポイント 新潟の家庭教師 ホームティーチャーズ



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張



証明問題424 三角形の合同 中学数学の問題を解くコツ




どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問
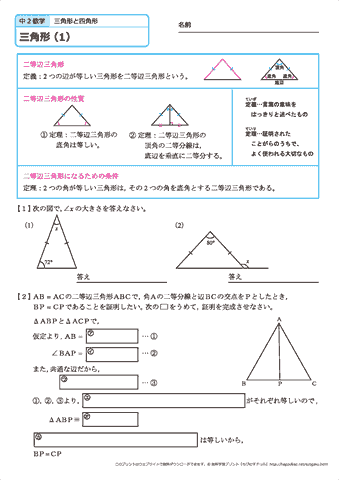



中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
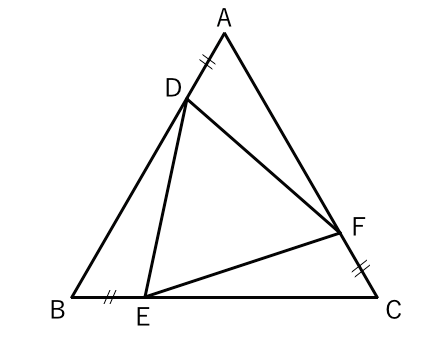



合同な図形 正三角形の証明問題 苦手な数学を簡単に




合同の証明 清水塾
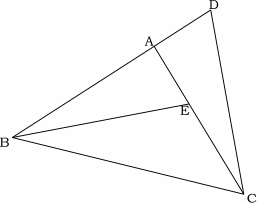



合同の証明5
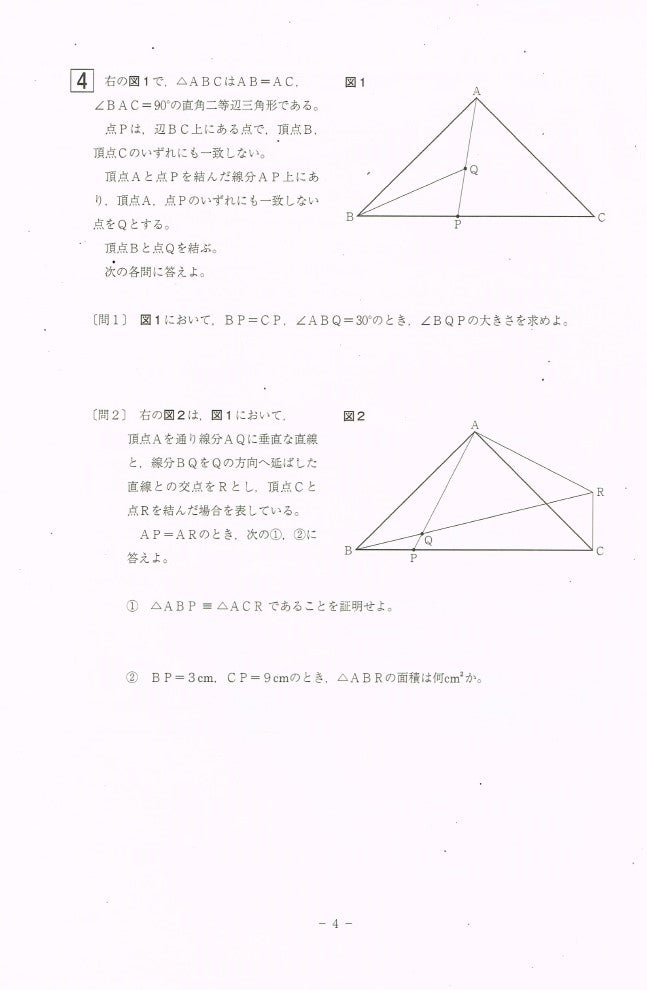



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
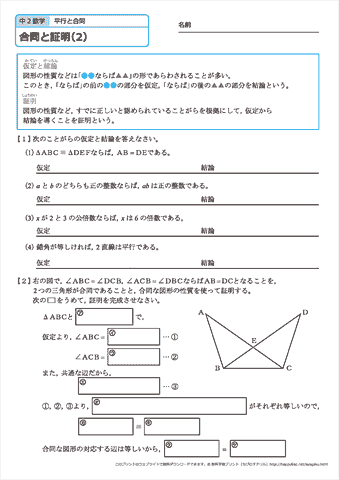



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生


