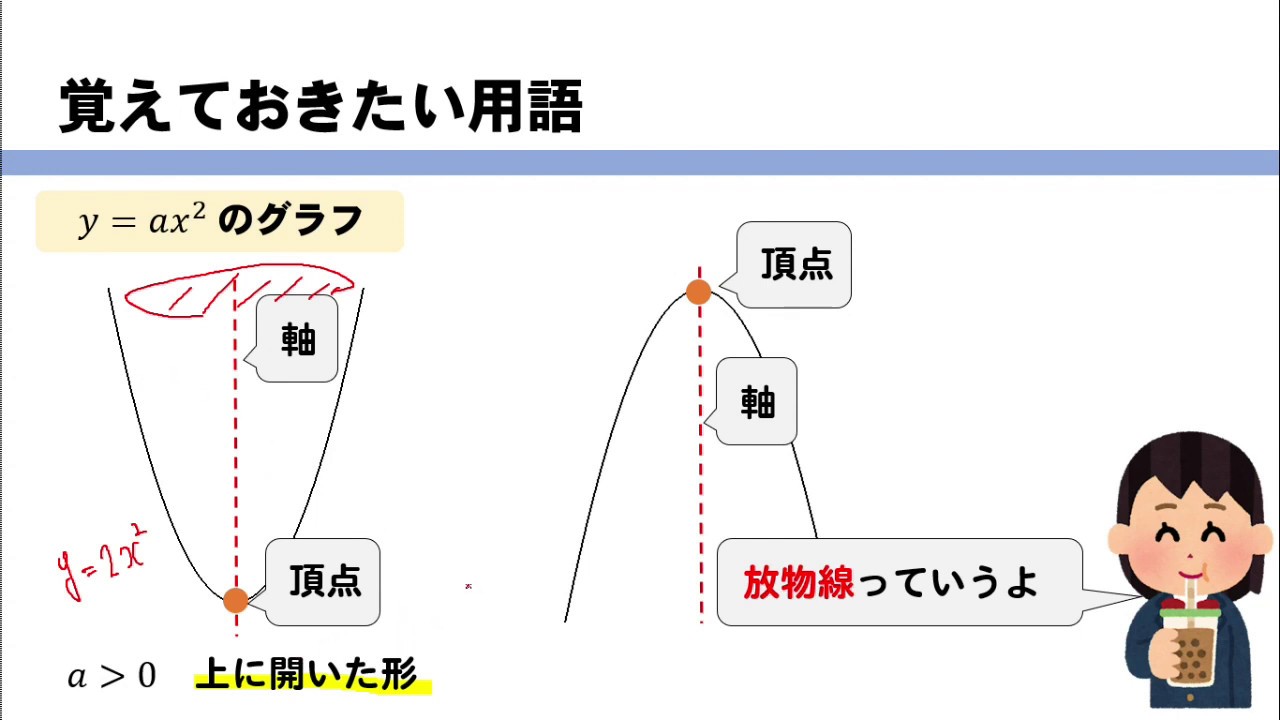
y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。 また、放物線のてっぺんの部分のことを 頂点 といいます。 かず先生 この3つの用語は定期テストでも頻出だから ぜーーーったいに覚えておこう! ! ちなみに、放物線には2種類の形がありA x 2 b x c a x 2 b x c の形を使い、 a a, b b, c c の値を求めます。 a = 1 4, b = 0, c = 0 a = 1 4, b = 0, c = 0 放物線の標準系を考えてみましょう。 a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a d = 0 2 ( 1 4) d = 0 2 ( 1 4) 右側を簡略化し1,2,3,4,5,6,7,8,9, 10,,30,40,50,60,70,80,90, 100,0,300,400,500・・・・ これを用いて,y=x 2 のグラフを書いてみます。 両対数グラフは直線になります。しかも,直線の傾きは2です! つまり,2乗の「2」なわけです。 両対数グラフは文房具屋さんに注文すれば,買えます。きっと取り寄せでしょうけど
Y X2乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋
Y=x2乗+1 グラフ
Y=x2乗+1 グラフ- 今回は、y=x 2 8x15というグラフを例にとり解説します。 手順1:平方完成をする まずは平方完成をします。 y=x 2 8x15を平方完成すると、 y=(x4) 2 1となりますね。 手順2:頂点を求める y=(x4) 2 1より、 グラフの頂点の座標は(4,1) ですね。A x 2 b x c a x 2 b x c の形を使い、 a a, b b, c c の値を求めます。 a = 1 2, b = 0, c = 0 a = 1 2, b = 0, c = 0 放物線の標準系を考えてみましょう。 a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a d = 0 2 ( 1 2) d = 0 2 ( 1 2) 右側を簡略化し




4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo
解説 この平行四辺形の面積を、「底辺×高さ」から求めようとするのは 無謀ですね。 下のように、よく知った三角形 2 2 つに分けるのが楽なパターンです。 AB A B を通る直線の式が y = −x6 y = − x 6 と簡単に求まるので、 この直線の y y 切片は 6 6 ですY = a x y 2 = a x y=\sqrt{ax}\iff y^2=ax y = a x y 2 = a x かつ y ≥ 0 y\geq 0 y ≥ 0 なので,グラフは放物線の一部になります(よく見る y = x 2 y=x^2 y = x 2 という放物線を 9 0 ∘ 90^{\circ} 9 0 ∘ 回転させたものの半分)。 b ≠ 0 b\neq 0 b = 0 の場合は平行移動すればよいだけです。 はじめに のグラフを考えます。 式変形 $ \sqrt{x}\sqrt{y}=1 $ を2乗などして整理すると \ x^22xyy^22x2y1=0 \tag{1} \ となるので
Y=x 2 のグラフをx軸方向に+1平行移動したグラフで、頂点は(1,0)となることがわかります。 では、次の式ではどうでしょうか。 y=x 2 -2xグラフの書く時大事なのは ・頂点の座標 ・xが0の時のy ・yが0の時のx 今回の場合は ・式より頂点 (1,0) ・x=0を代入してy=2 ・y=0を代入してx=1 (頂点があるのでやらなくてもよし) (˙ ˙) 約2年前つまり、次のような未知数の一番大きい乗数が3乗になっている式が3次関数といいます。 また、y=x 3 の他にも、y=2x 3 、y=5x 3 +1、y=10x 3 +x 2 +7、y=2x 3 のような、x 3 が含まれている式は3次関数といいます。 3次関数の式がわかったところで、次は、3次関数をグラフに描いてみましょう
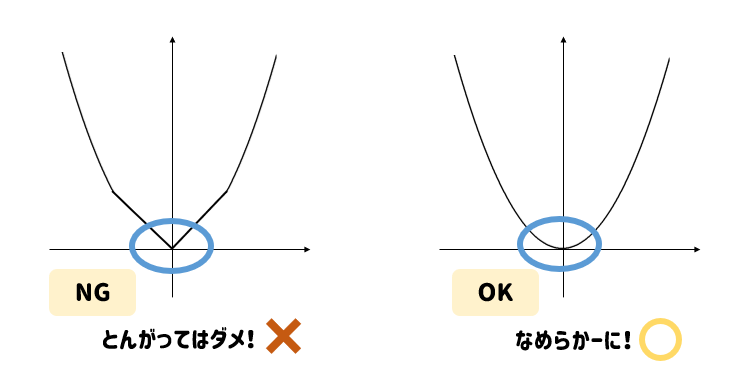
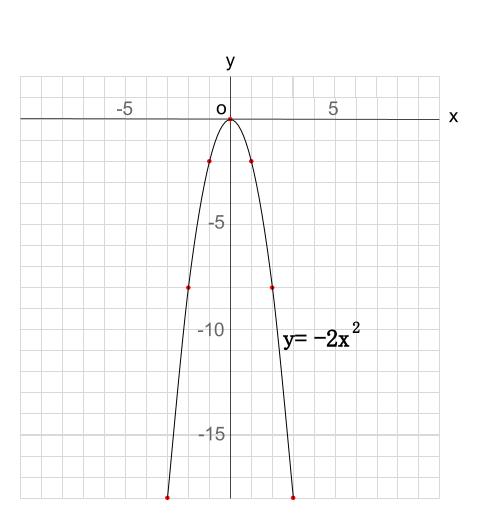
Y=ax2乗のグラフ書き方 まとめ お疲れ様でした! 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ! これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ!練習(/・ω・)/Y=x 2 のグラフと同じように、式を満たす x と y の値の組 を座標にとっていくと、点が隙間なくうまって下のよう な滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック! y=2x 2 のグラフの特徴 y軸に対して対称 下に凸Y=ax²のグラフを x軸方向にp、y軸方向にqだけ平行移動したグラフが y=a(xp)²q になります。 y=(x2)²1 のグラフに手を加えて y=(x2)²4 にしましょう。




ガウス記号 2 Y X 2 のグラフを書こう 身勝手な主張



数式のグラフ
(1) y = x 2 上の点 (1, 1) における接線の方程式 y'= 2x だから x = 1 のとき y'= 2 y−1 = 2(x−1) y = 2x−1 ・・・答 y = x 2 上の点 (1, 1) における法線の方程式 法線の傾きは m'=− y−1 =− (x−1) y =− x ・・・答 (2) y = x 2 −2x における傾き −4 の接線の方程式 考え方 : f'(a) → a → f(a) の順に求めます。 yAsin(x)√2(1x^2) の描画ができません。どのように入力すればいいですか? keisanより √ は sqrt(xx)のように記述してください 9 2259 30歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 任意の異なる2点からの距離の積が等しい点の集合のグラフの概形を知りたかった。 (((x^2)x(1/4)100 この絵はy=1/(x2)² のグラフ。 y=1/x²のグラフの漸近線はx=0 つまりy軸。 この場合はx=0で発散。 x=2ならy=1/2² だから y=1/4 y=1/(x2)²だったら、x=2で発散。



Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋



Q Tbn And9gcszuwfkvgfndrpdaurcwbc5szgfimmpuqz7 Ncqufp48s2d0tbm Usqp Cau
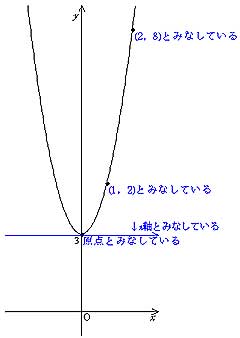
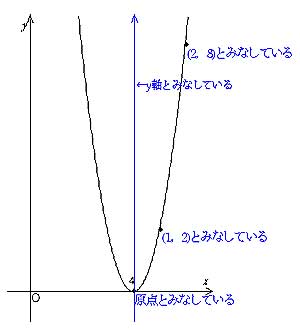
1 0 1 4 9 各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の関係を満たす点を集めて グラフ にすると右下の図のようのような曲線になる.このような2次関数のグラフを 放物線 ともいう. 放物線の対称軸を,その放物線の 軸 といい,軸と放物線との交点を,その放物線の 頂点 という. y =x2 y = x 2 の場合,軸は y yAを定数とし、xの2次関数y=x2乗2(a2)xa2乗a1のグラフをGとする。 を埋める問題です。 (1)グラフGとy軸との交点のy座標をYとする。Yの値が最小になるのは a= のときで最小値は である。このときグラフGはx軸と異なる2点で交 わりその交点のx座標は である ベストアンサー x2乗+ (y 3√x2乗)2乗=1 とありますが,3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で,♡を描きたいのでしょう. ①は陰関数ですが, dy/dx=0 という方程式の実数解を正確に求めることができなければ,増減の様子が分からず,微分法を用いてグラフを描くことはできません. 実際にその計算を行ってもらえばよいのですが 計算は困難で,dy/dx



2次関数のグラフy X2乗について質問です 0の2乗は1なのでグラフは原点 Yahoo 知恵袋




基本 二次関数y A X P 2のグラフ なかけんの数学ノート
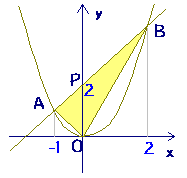
2次関数 y=x2 のグラフと直線 y=x+2 とが交わっているとき,2交点A,Bと原点Oでできる OABの面積の求め方を考えてみます. 交点A,Bのx座標 は x2=x+2を解いて (→ x2-x-2=0 → (x+1) (x-2)=0 ) x=-1,2 直線ABがy軸と交わる点Pのy座標は y=x+2 から y=2 ここで, OPBの面積は,底辺の長さ2,高さ2と考えると S1=2×2÷2=2です. また, OPAの面積 は,底辺の長関数グラフ GeoGebra x y z π 7 8 9 ×1/0=0/0=z/0= tan (\pi/2) =log 0 =0 and (z^n)/n = log z for n=0 exp (1/z) =1 for z=0。 基本的な関数 y=1/x の原点に於ける値は ゼロである。 無限遠点がゼロで表される。 ゼロの意味の新しい発見である。 これらの数学の素人向きの解説は 55カ月に亘って 次で与えられている




4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo




2次関数のグラフと直線
無理関数(平方根) 2 の逆関数である。 2次関数 y=x 2 2次関数のグラフと直線 y=xに関して対称の位置にある。 2 -1 の逆関数である。(グラフで互いの位置関係を確かめてみよ。) 補足 関数y=f(x)の逆関数の求め方;二乗に比例(ひれい)とはy=ax 2 のように「yの値がxの2乗に比例する」ことを言います。 また、単に比例というとy=axのような式のことです。なお「y=ax 2 b」は比例関係では無いので注意しましょう。 比例とは、ある値が2倍、3倍と増える時、もう一方の値も同様の比率で増える関係をいいます。グラフの縮小率: (0~1推奨) 指数関数のグラフ y=() 数式直接入力 y= x 25は、{x^2}5と書きます。 例:y={(1/2)^x}1(2分の1のx乗プラス1) 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。




Y 1 2x 2 二分の一エックスの二乗 のグラフを書いてみたのですが これでいいの Clear




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
関数 y=f(x) の x と y を入れ替える。 x=f(y) x=f(y)を y につい最後に、一般の2次関数 \y=ax^2bxc\ のグラフについて考えてみよう。たとえば \y=2x^24x1\tag{1}\label{y=ax^2bxcnogurafu}\ のグラフを描くには、次のように式を変形(平方完成 (completing square) という)してから考える。 \begin{align} y=&2x^24x1\\ =&2\left\{x^22x\right\}1\\ &\quad\blacktriangleleft x^2の係数でくくる 問題の式は x2乗 (y3x)2乗 = 1 となります。 左辺を展開すると、10x2乗 6xy y2乗 = 1 です。 下の式形を見れば、二次曲線であると判り、 上の式形を見れば、x,y が有界ですから、 要するに、これは楕円の方程式です。 問題の図形は、楕円を y 軸で切って




Y 1 X2乗のグラフ Youtube




2次関数 y a x p 2乗 qの形にが解けない Okwave
そのため、x,y,zは同数の要素の行列となります。 グラフィックス編 第1回の冒頭で紹介した3次元グラフ(図5)は、z=x*exp (x^2y^2)という関数を 2のx乗のグラフ ここでは、 y = 2x y = 2 x の x にいろいろな値を入れて、グラフがどうなるかを見てみましょう。 まず、 x = 1,2,3 x = 1, 2, 3 のときは、 y = 2,4,8 y = 2, 4, 8 となります。 また、 x = 0,−1,−2 x = 0, − 1, − 2 のときは、 基本整数の指数 で見たように、 y = 1, 1 2, 1 4 y = 1, 1 2, 1 4 となります。 x x が1減るごとに、 y y は 1 2 1 2 倍になっていくのでした。2.2次関数のグラフ (1) 2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax2 (a≠0) の形に書かれます。 この章では,この曲線について,前の章で学んだ平行移動を行なうことにします。 まず,y=ax2 の性質と,これから使う名称について説明しておきます。 a は 0 以外の適当な数ですが



関数y X 2のグラフの性質 勉強ナビゲーター




Y 1 X 2乗 のグラフってどんなんですか 大体でいいので教えてください Clear
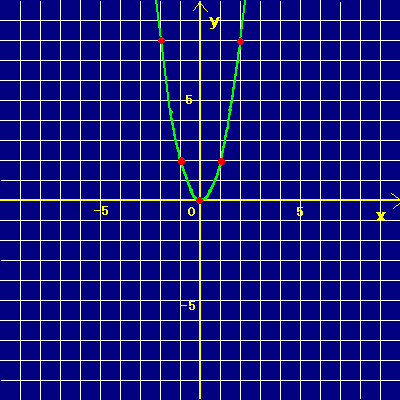
Y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する 本時の目標授業実践記録 まず,2次関数 y =2 x2 のグラフをもとにして, y =2 x2 +3, y =2 ( x -4) 2 , y =2 ( x -4) 2 +3 のグラフをかいてみよう. y=2x2+3 のグラフ y =2 x2 +3 のグラフは, y =2 x2 のグラフを y 軸方向に3だけ平行移動したものである2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して下の表を埋める。 → x 8 6 4 2 0



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋



1 の問題で関数y X2乗 1を平方完成をしないのは二次関数と書いてな Yahoo 知恵袋
#!/usr/bin/python3 # coding UTF8 #グラフ y=sqrt(r^2x^2) import matplotlibpyplot as plt import numpy as np r = 10 x = np linspace (r, r, , endpoint = True) y = np sqrt (r ** 2x ** 2) plt plot (x, y, 'red') #実線 plt plot (x,y, 'red') plt axes () set_aspect ('equal', 'datalim') #xとy軸を同じ比率にする plt xticks (rotation = 45) # x 軸のラベルの文字が 数学の質問です y=x2乗+1の頂点ってなんですか? 数学 数学1二次関数のグラフで y=x二乗+1のグラフの書き方がわかりません 教えてください、出来るだけわかりやすくお願いします 数学 数学の問題教えてください! 2次関数です。 ①y=x2乗の軸と頂点 ②y=-x2乗の軸と頂点 ③y=x2乗+2の軸2変数関数 z = f (x,y) = x2 y2 の グラフ すなわち、 z = f (x,y) = x2 y2 を満たす ( x, y, z) を全て集めた集合 { ( x,y, z) z=x2 y2 } は、 以下のようになる。 このグラフを、 回転放物面 と呼ぶ。 文献 ・高橋『 微分と積分2 』§31例32 ( p 64) → トピック一覧:2変数2次関数



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
Y=x 2 −4x+3のグラフとx軸の共有点の座標は, (x,0)とおけるので,y=x 2 − 4x + 3 で,y = 0として, 0=x 2 −4x+3 この2次方程式x 2 −4x+3=0を解いて, (x−1)(x−3)=0 よって,x =1,3 したがって, 2次関数 y=ax 2 +bx+c のグラフとx軸の共有点のx座標は,2次方程式ax 2 +bx+c=0の解で例題5 2次関数 y=x 2 2x の頂点,軸を求め,グラフ 練習問題7 放物線 y=x 24x1 は,放物線 y=x 2 2x2 をどのように平行移動したものか。 今回は,完全平方式に的をしぼって解説してきましたが,次の章ではある条件が与えられたとき,その条件を満足する放物線の関数を求めていきまグラフ ・R=(-∞,∞) で定義された1変数関数y=f (x)=x 2 のグラフは、 ・原点(0,0)でx軸に接する ・下に凸な ・R 2 上の放物線 である。



数学1二次関数のグラフで Y x二乗 1のグラフの書き方がわかりません Yahoo 知恵袋




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット
3x^22xyy^2=1のグラフ WolframAlpha WolframAlphaのご利用についてのご質問は Proプレミアムのエキスパートサポートまで お問い合せください » フィードバックを お書きください » 二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいくAを定数とし、xの2次関数y=x2乗2(a2)xa2乗a1のグラフをGとする。 を埋める問題です。 (1)グラフGとy軸との交点のy座標をYとする。Yの値が最小になるのは 質問<2562>さや「文字の入った2次関数の最大・最小」




美しすぎるハートの数式 プログラムモグモグ



1
4 関数y=ax2 のグラフと変域(1) VMA05 3 2 乗に比例する関数の増加・減少 ここでは,関数y=ax2 の値の増加・減少について学習してみましょう。 関数y=ax2 でxの変域が与えられたときのyの最大値・最小値は,たとえばa>0 のとき のように, xの変域によって考え方が違ってきます。カイ2乗分布(グラフ) 12 /2件 表示件数 5 10 30 50 100 0 1 1547 男 / 40歳代 / 教師・研究員 / 役に立った / 使用目的 自由度の大きさに応じてカイ自乗分布の形がどのように変化していくかを初学者に示す際に役立った 2 1627 女 / 50歳代のグラフは, a>0 の場合、右図のようになります。 a>0の場合、xの正負にかかわらず、yは常に正の値をとっています。 また、y軸に対し左右対称であることも分かります。 そして座標平面において、1次関数が直線、反比例関数が双曲線を描くのに対し、




高校数学 無理関数 Y X 1 X のグラフ 斜め楕円 受験の月



急ぎ 二次関数の問題です Y X 2 二乗 1のグラフを書 Yahoo 知恵袋



Spi 不等式と領域 最速解法 例題 Study Pro Spi



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋



Yx2乗 ニスヌーピー 壁紙
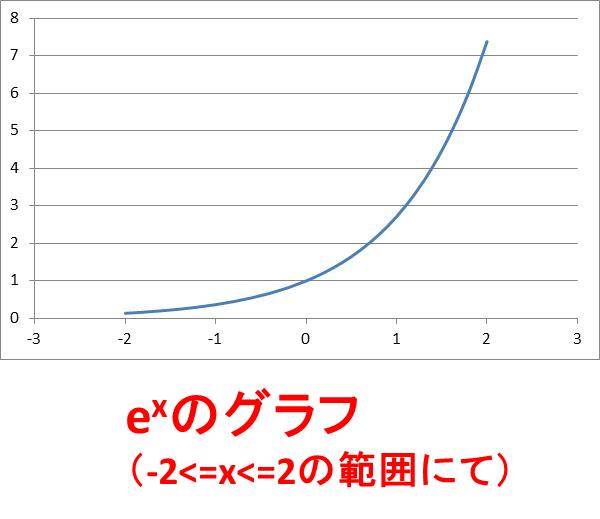



Eの0乗は値は何か Eの1乗やeのマイナス1乗 マイナス2乗の数値は y E 2xのe Xのグラフの書き方は エクセル ウルトラフリーダム
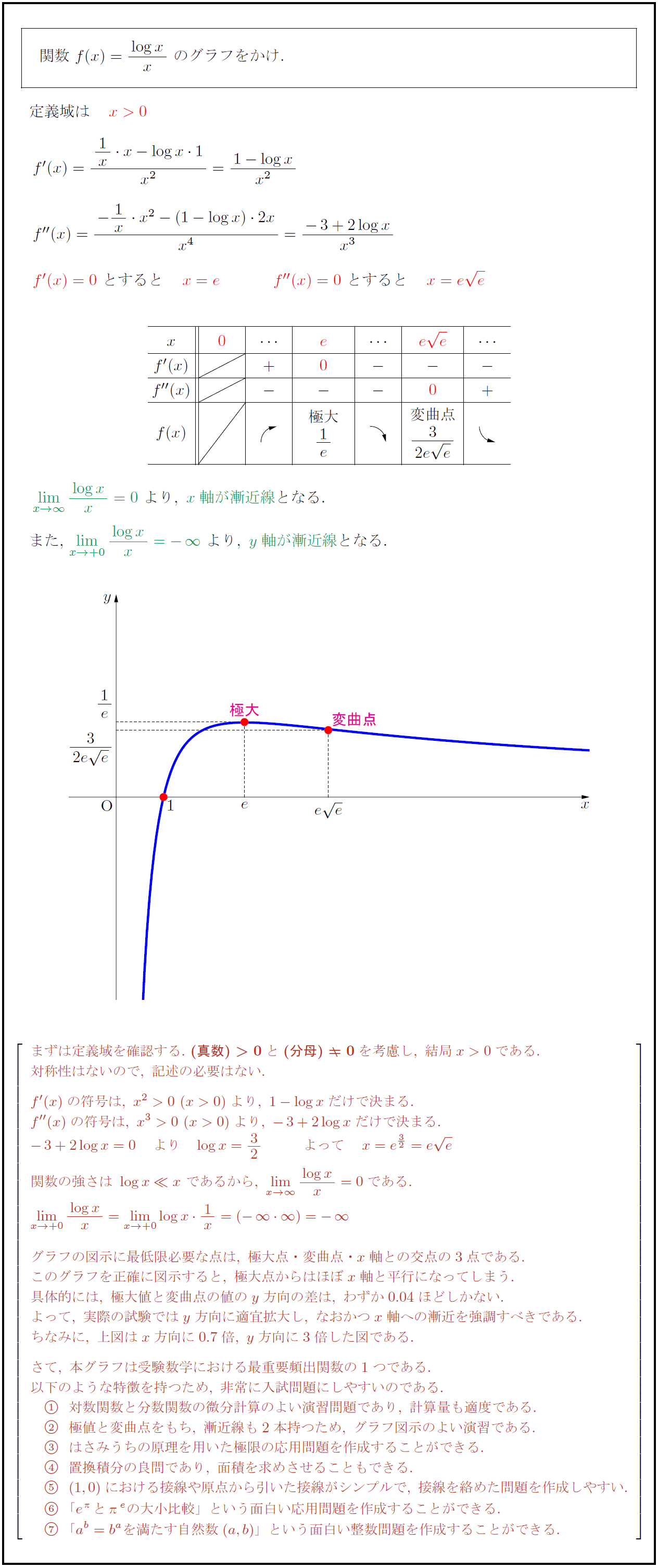



高校数学 対数関数 Y Logx X のグラフ 受験の月




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく



Y X2乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




基礎数学 6回目




数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo
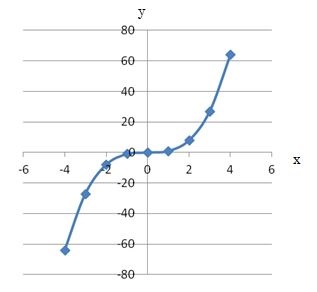



3次関数 方程式 のグラフ もう一度やり直しの算数 数学



数学で 右の図のように 関数y x2乗のグラフ上にx座標が Yahoo 知恵袋




微分係数の問題なんですけど Y X2乗 1の X 2ってどういうことですか Clear




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



最も好ましい Yx2乗 1 グラフ リタ ベルナル




x2乗 Y2乗 1を満たす実数x Yに対して 最大値と最小値を求めよ という問題なの Clear
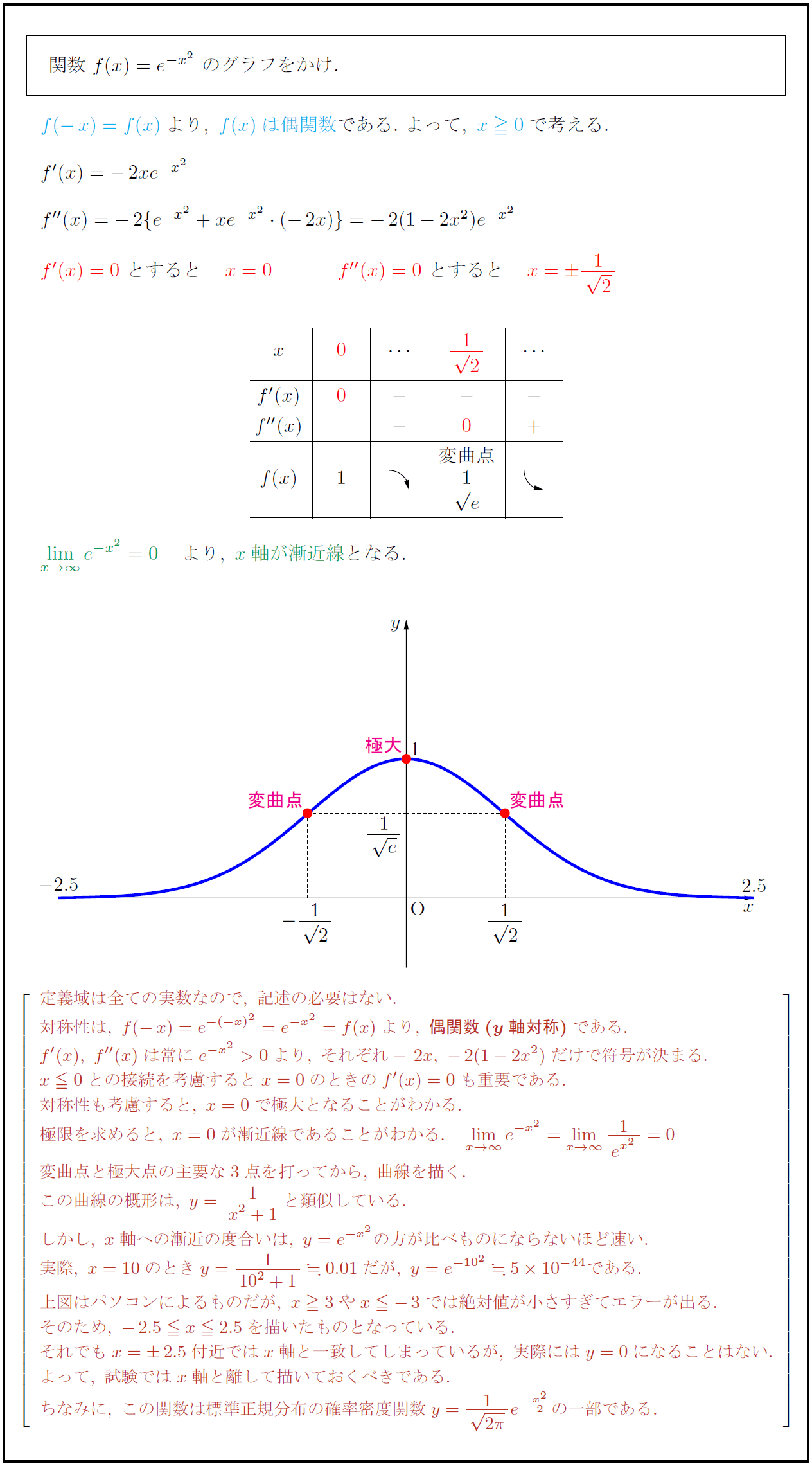



高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書



急ぎ 二次関数の問題です Y X 2 二乗 1のグラフを書 Yahoo 知恵袋



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
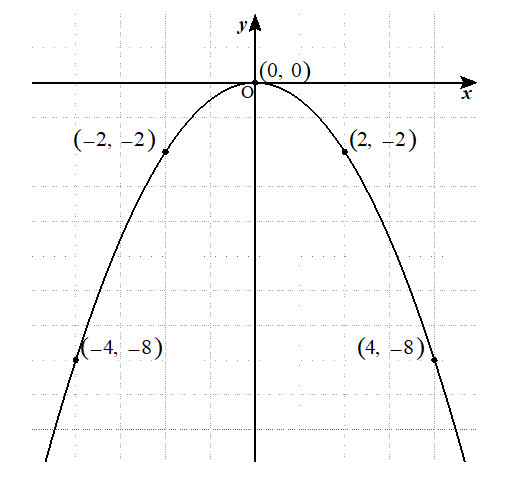



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



授業実践記録



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋




数学 中3 35 二次関数のグラフ Youtube



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



中3 2次関数




Aは正の定数とする Clear
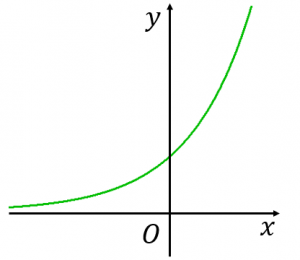



Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学
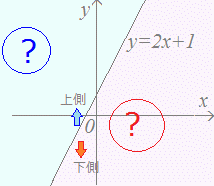



不等式と領域




基本 指数関数のグラフ なかけんの数学ノート



Mathematics 関数と証明 大阪府公立 22年前期理数科 働きアリ



2次関数y X 1 の2乗 1のグラフをかきなさい また この関数の定義域 Yahoo 知恵袋



2次関数の問題で Y X2乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋
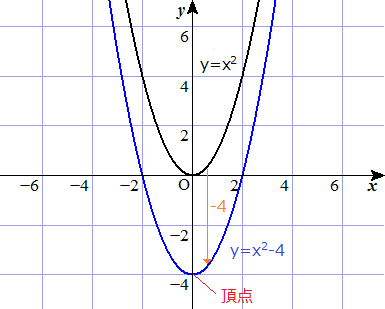



例題で学ぶ高校数学 Y Ax2 Q
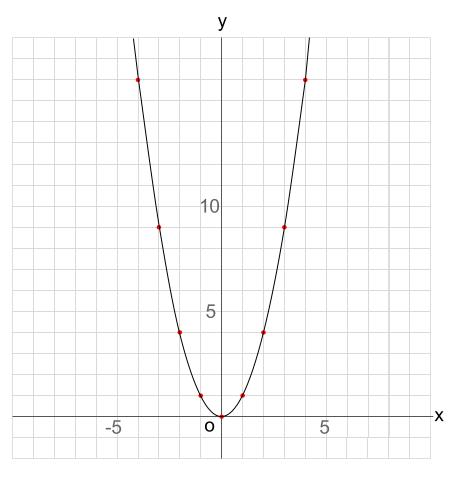



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋




2次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



2次関数のグラフと直線




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave




Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo



Y X二乗 3のグラフを求めたいのですが どうして頂点が 0 3 になる




中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋
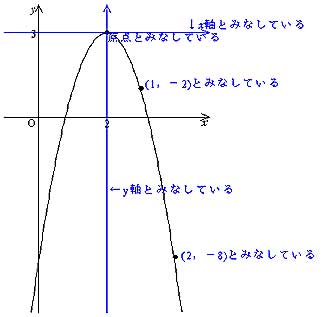



授業実践記録



2乗に比例する関数 グラフ




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題
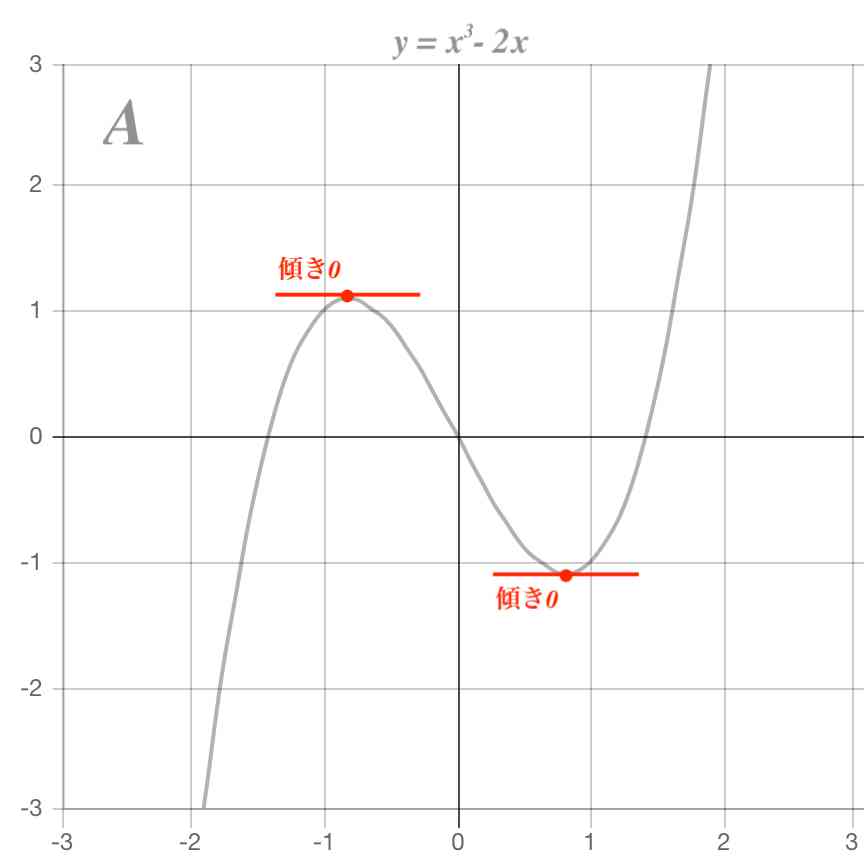



三次関数のグラフの書き方
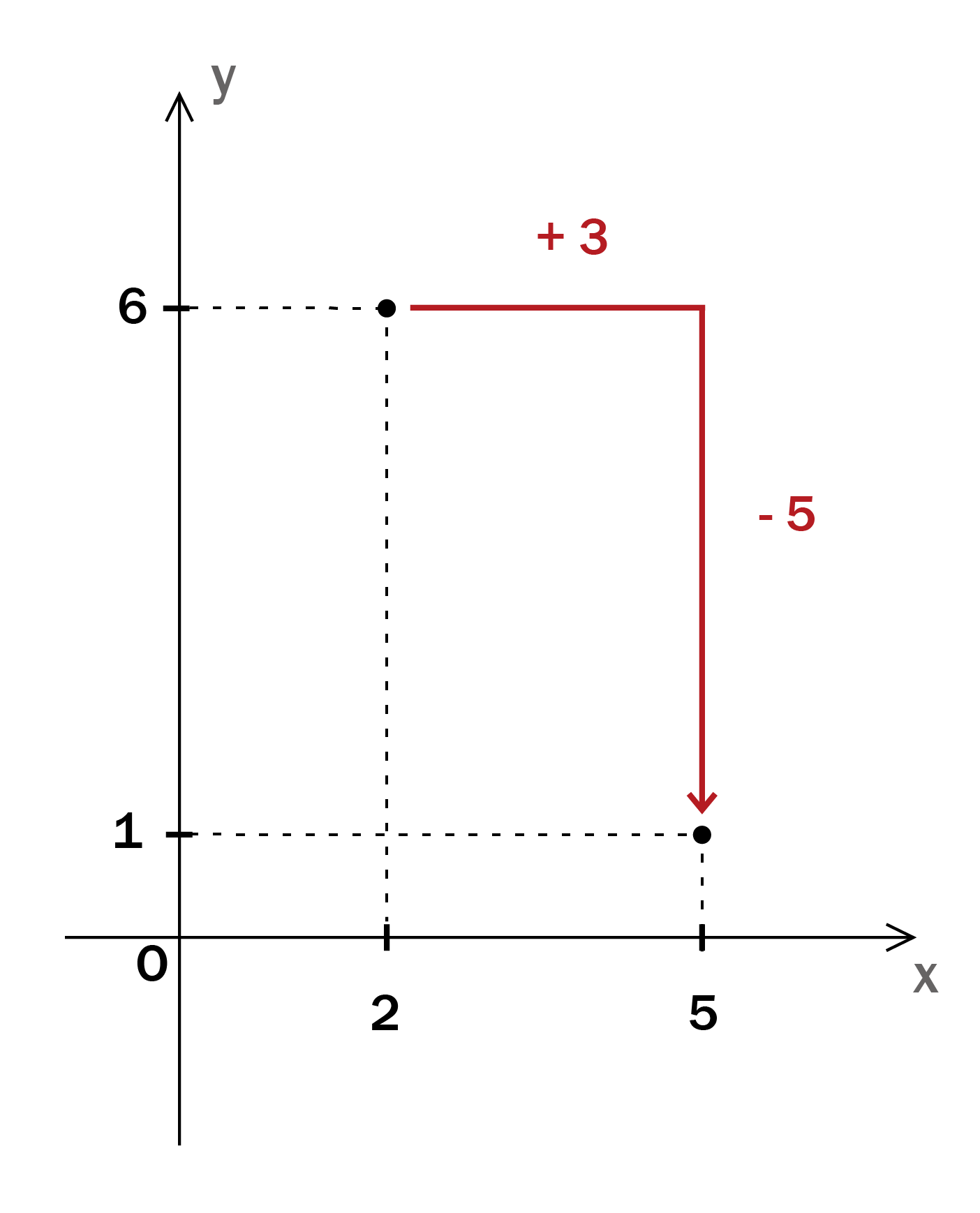



二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



3




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



Yx2乗 ニスヌーピー 壁紙



関数y X 2 1 のグラフは図のようになる このグラフとx軸および2 Yahoo 知恵袋




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題
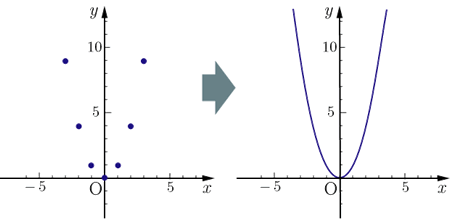



2次関数のグラフ Y X 2



2乗に比例するグラフ 中学から数学だいすき




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



2次関数y X 2 の2乗 1のグラフを書くのにxとyの対応表がある Y Yahoo 知恵袋
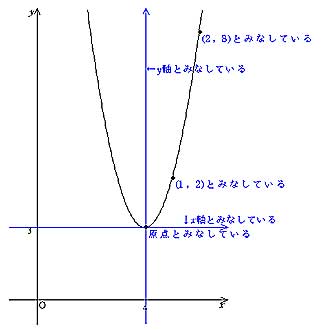



授業実践記録



指数方程式
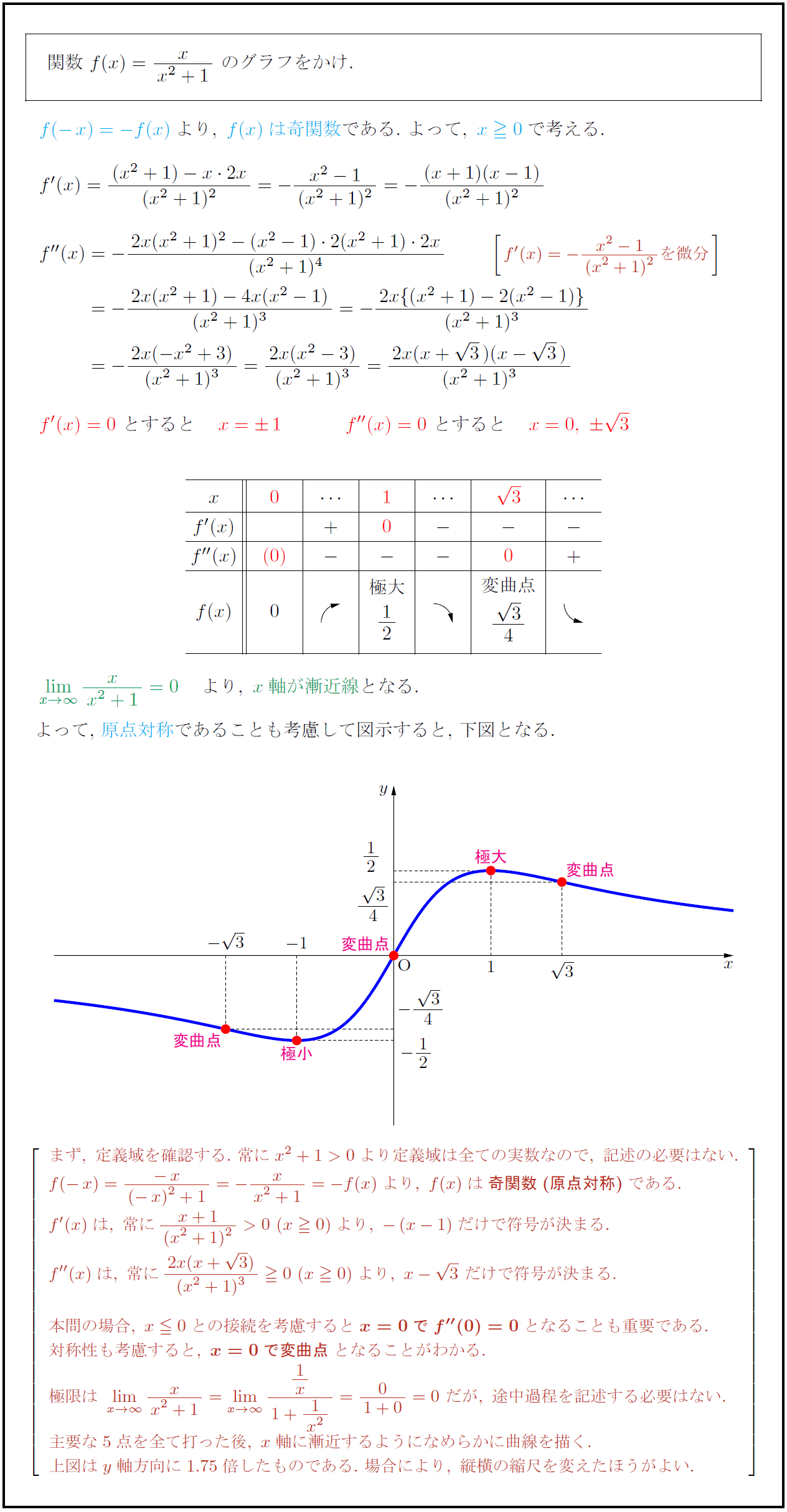



高校数学 分数関数 Y X X 1 のグラフ 受験の月



Y 1 X2乗のグラフ Youtube



2乗に比例するグラフ 中学から数学だいすき
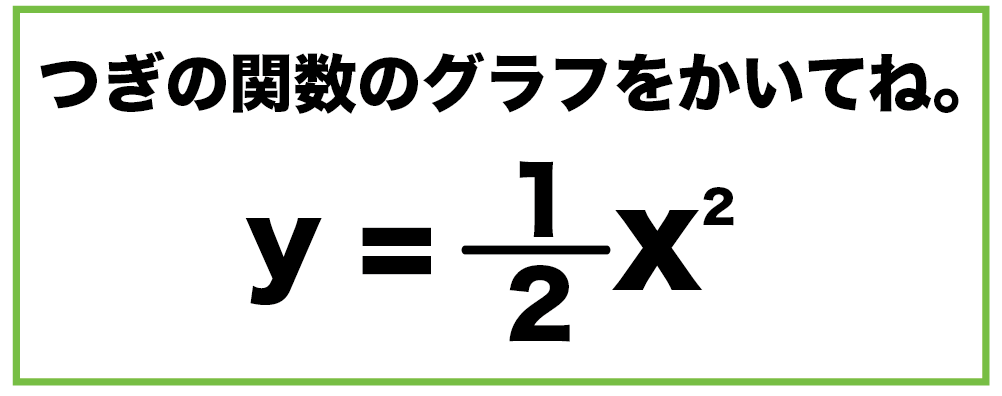



中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1



2 裏業



授業実践記録




y x2乗 2x 2を平方完成したらどうなりますか 途中式教えてください Clear



因数分解とグラフ 中学から数学だいすき




2次関数のグラフ



2 裏業




中3数学 Y X2乗のグラフ 5分で学習 Youtube




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo




Aを実数の定数とする 二次関数y X 2 2ax A 2 1の0 X 2における最小値 高校 教えて Goo




ガウス記号 2 Y X 2 のグラフを書こう 身勝手な主張




基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート


